
分析 (1)分别求出不等式组中两不等式的解集,找出解集的公共部分即可;
(2)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,求出已知方程的解得到a的值,代入计算即可求出值.
解答 解:(1)$\left\{\begin{array}{l}{2x+5≤3(x+2)①}\\{\frac{x-1}{2}<\frac{x}{3}②}\end{array}\right.$,
由①得:x≥-1,
由②得:x<3,
则不等式组的解集为:-1≤x<3;
(2)原式=$\frac{a(a-2)}{(a+1)(a-1)}$÷$\frac{{a}^{2}-1-2a+1}{a+1}$=$\frac{a(a-2)}{(a+1)(a-1)}$•$\frac{a+1}{a(a-2)}$=$\frac{1}{a-1}$,
方程x2+x=6,解得:x=-3或x=2(舍去),
当a=x=-3时,原式=-$\frac{1}{4}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,△ABC中,∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B,C点重合),∠ADE=45°.求证:△ABD∽△DCE.
已知:如图,△ABC中,∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B,C点重合),∠ADE=45°.求证:△ABD∽△DCE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
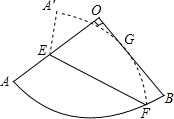 如图,已知扇形AOB的半径为6,圆心角为90°,E是半径OA上一点,F是$\widehat{AB}$上一点.将扇形AOB沿EF对折,使得折叠后的圆弧$\widehat{A′F}$恰好与半径OB相切于点G,若OE=5,则O到折痕EF的距离为$\sqrt{15}$.
如图,已知扇形AOB的半径为6,圆心角为90°,E是半径OA上一点,F是$\widehat{AB}$上一点.将扇形AOB沿EF对折,使得折叠后的圆弧$\widehat{A′F}$恰好与半径OB相切于点G,若OE=5,则O到折痕EF的距离为$\sqrt{15}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
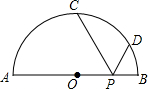 如图,AB是半径为R的半圆的直径,C、D是半圆周上的两点,已知$\widehat{AC}$、$\widehat{BD}$的度数分别是90°和30°,动点P在线段AB上,则PC+PD的最小值是$\sqrt{3}$R.
如图,AB是半径为R的半圆的直径,C、D是半圆周上的两点,已知$\widehat{AC}$、$\widehat{BD}$的度数分别是90°和30°,动点P在线段AB上,则PC+PD的最小值是$\sqrt{3}$R.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
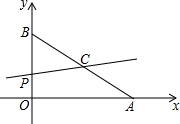 如图,平面直角坐标系中,已知点A(4,0)和点B(0,3),点C是AB的中点,点P在折线AOB上,直线CP截△AOB,所得的三角形与△AOB相似,那么点
如图,平面直角坐标系中,已知点A(4,0)和点B(0,3),点C是AB的中点,点P在折线AOB上,直线CP截△AOB,所得的三角形与△AOB相似,那么点查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a>b>c | B. | c>b>a | C. | b>c>a | D. | c>a>b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com