
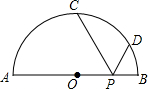
 如图,AB是半径为R的半圆的直径,C、D是半圆周上的两点,已知$\widehat{AC}$、$\widehat{BD}$的度数分别是90°和30°,动点P在线段AB上,则PC+PD的最小值是$\sqrt{3}$R.
如图,AB是半径为R的半圆的直径,C、D是半圆周上的两点,已知$\widehat{AC}$、$\widehat{BD}$的度数分别是90°和30°,动点P在线段AB上,则PC+PD的最小值是$\sqrt{3}$R. 分析 根据轴对称,作出点D关于AB的对称点E,连接CE交AB于点P,此时PC+PD最小,就等于CE的长.由题意可知∠COE=120°,然后在△COE中求出DE的长.
解答 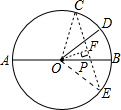 解:设点D关于AB的对称点为E,连接CE交AB于P,则此时PC+PD的值最小,且PC+PD=PC+PE=CE.连接OC、OE;
解:设点D关于AB的对称点为E,连接CE交AB于P,则此时PC+PD的值最小,且PC+PD=PC+PE=CE.连接OC、OE;
∵弧AC的度数为90°,弧BD的度数为30°;
∴弧CB的度数为90°;
∴弧CBE的度数为120°,即∠COE=120°;
过O作OF⊥CE于F,则∠COF=60°;
Rt△OCF中,OC=R,∠COF=60°;因此CF=$\frac{\sqrt{3}}{2}$R;
∴CE=2CF=$\sqrt{3}$R,即PC+PD的最小值为$\sqrt{3}$R.
故答案为:$\sqrt{3}$R.
点评 本题考查的是垂径定理,根据轴对称找出点D的对称点点E,由两点之间线段最短,确定CE的长就是PC+PD的最小值,然后由题目所告诉弧的度数得到∠COE的度数,在△COE中求出CE的长.


科目:初中数学 来源: 题型:选择题
| A. | 2,2 | B. | 2,3 | C. | 3,4 | D. | 4,4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ①③④ | C. | ①②④ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com