
| A. | ①② | B. | ①③④ | C. | ①②④ | D. | ①②③④ |
分析 ①求出抛物线与y轴的交点即可判断;
②根据两抛物线对称轴相同,可知其中一条抛物线经过向上或向下平移得到另一条抛物线;
③根据两抛物线对称轴相同,可知两条抛物线不可能左右平移得到;
④配方后得到顶点坐标,相减即可.
解答 解:①P与y轴交点为(0,-m2),Q与y轴交点为(0,-(m2+1)),一定不在x轴的上方,故本选项正确;
②由于两抛物线对称轴相同,均为x=m,可知,其中一条抛物线经过向上或向下平移得到另一条抛物线;故本选项正确;
③由于两抛物线对称轴相同,两条抛物线不可能左右平移得到,故本选项错误;
④P配方得,y=x2-2mx+m2-2m2=(x-m)2-2m2;Q配方得,y=x2-2mx+m2-m2-m2-1=(x-m)2-2m2-1,-2m2-(-2m2-1)=1,故本选项正确.
故选C.
点评 本题考查了二次函数的性质,熟悉二次函数与x轴、y轴的交点的求法,图象的平移、顶点坐标的求法是解题的关键.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:解答题
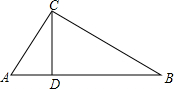 如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若∠B=32°,CD=6,求AB的长.(结果保留到0.1)(已知sin32°=0.5299,cos32°=0.8480,tan32°=0.6249)
如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若∠B=32°,CD=6,求AB的长.(结果保留到0.1)(已知sin32°=0.5299,cos32°=0.8480,tan32°=0.6249)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
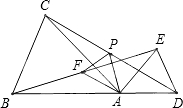 如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,点B、A、D在同一条直线上,连接BE、CD,F、P分别为BE、CD的中点,连接AF、AP、PF.
如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,点B、A、D在同一条直线上,连接BE、CD,F、P分别为BE、CD的中点,连接AF、AP、PF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
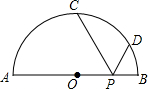 如图,AB是半径为R的半圆的直径,C、D是半圆周上的两点,已知$\widehat{AC}$、$\widehat{BD}$的度数分别是90°和30°,动点P在线段AB上,则PC+PD的最小值是$\sqrt{3}$R.
如图,AB是半径为R的半圆的直径,C、D是半圆周上的两点,已知$\widehat{AC}$、$\widehat{BD}$的度数分别是90°和30°,动点P在线段AB上,则PC+PD的最小值是$\sqrt{3}$R.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
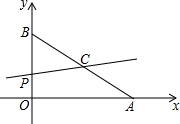 如图,平面直角坐标系中,已知点A(4,0)和点B(0,3),点C是AB的中点,点P在折线AOB上,直线CP截△AOB,所得的三角形与△AOB相似,那么点
如图,平面直角坐标系中,已知点A(4,0)和点B(0,3),点C是AB的中点,点P在折线AOB上,直线CP截△AOB,所得的三角形与△AOB相似,那么点查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 注入水的时间t(分钟) | 0 | 10 | … | 25 |
| 水池的容积V(公升) | 100 | 300 | … | 600 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com