
分析 设t=$\sqrt{\frac{{a}^{2}{b}^{2}}{(a-b)^{2}}+\frac{{b}^{2}{c}^{2}}{(b-c)^{2}}+\frac{{c}^{2}{a}^{2}}{(c-a)^{2}}}$,并设t是无理数,然后得到t2也是无理数,然后根据a、b、c是三个不同的有理数得出矛盾,利用反证法求解即可.
解答 解:设t=$\sqrt{\frac{{a}^{2}{b}^{2}}{(a-b)^{2}}+\frac{{b}^{2}{c}^{2}}{(b-c)^{2}}+\frac{{c}^{2}{a}^{2}}{(c-a)^{2}}}$,并设t是无理数,
则有t2=$\frac{{a}^{2}{b}^{2}}{(a-b)^{2}}+\frac{{b}^{2}{c}^{2}}{(b-c)^{2}}+\frac{{c}^{2}{a}^{2}}{(c-a)^{2}}$是无理数,
∵a、b、c是三个不同的有理数,
∴$\frac{{a}^{2}{b}^{2}}{(a-b)^{2}}+\frac{{b}^{2}{c}^{2}}{(b-c)^{2}}+\frac{{c}^{2}{a}^{2}}{(c-a)^{2}}$是有理数,这与t2=$\frac{{a}^{2}{b}^{2}}{(a-b)^{2}}+\frac{{b}^{2}{c}^{2}}{(b-c)^{2}}+\frac{{c}^{2}{a}^{2}}{(c-a)^{2}}$是无理数矛盾,
∴t是有理数,
即$\sqrt{\frac{{a}^{2}{b}^{2}}{(a-b)^{2}}+\frac{{b}^{2}{c}^{2}}{(b-c)^{2}}+\frac{{c}^{2}{a}^{2}}{(c-a)^{2}}}$是有理数.
点评 本题考查了有理数、无理数的概念与运算,题目采用了反证法证明,利用反证法证明命题的第一步是假设命题不成立,难度不是很大.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,△ABC中,∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B,C点重合),∠ADE=45°.求证:△ABD∽△DCE.
已知:如图,△ABC中,∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B,C点重合),∠ADE=45°.求证:△ABD∽△DCE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
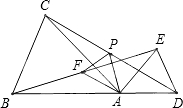 如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,点B、A、D在同一条直线上,连接BE、CD,F、P分别为BE、CD的中点,连接AF、AP、PF.
如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,点B、A、D在同一条直线上,连接BE、CD,F、P分别为BE、CD的中点,连接AF、AP、PF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
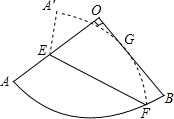 如图,已知扇形AOB的半径为6,圆心角为90°,E是半径OA上一点,F是$\widehat{AB}$上一点.将扇形AOB沿EF对折,使得折叠后的圆弧$\widehat{A′F}$恰好与半径OB相切于点G,若OE=5,则O到折痕EF的距离为$\sqrt{15}$.
如图,已知扇形AOB的半径为6,圆心角为90°,E是半径OA上一点,F是$\widehat{AB}$上一点.将扇形AOB沿EF对折,使得折叠后的圆弧$\widehat{A′F}$恰好与半径OB相切于点G,若OE=5,则O到折痕EF的距离为$\sqrt{15}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
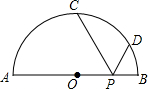 如图,AB是半径为R的半圆的直径,C、D是半圆周上的两点,已知$\widehat{AC}$、$\widehat{BD}$的度数分别是90°和30°,动点P在线段AB上,则PC+PD的最小值是$\sqrt{3}$R.
如图,AB是半径为R的半圆的直径,C、D是半圆周上的两点,已知$\widehat{AC}$、$\widehat{BD}$的度数分别是90°和30°,动点P在线段AB上,则PC+PD的最小值是$\sqrt{3}$R.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
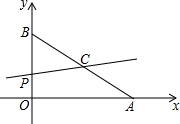 如图,平面直角坐标系中,已知点A(4,0)和点B(0,3),点C是AB的中点,点P在折线AOB上,直线CP截△AOB,所得的三角形与△AOB相似,那么点
如图,平面直角坐标系中,已知点A(4,0)和点B(0,3),点C是AB的中点,点P在折线AOB上,直线CP截△AOB,所得的三角形与△AOB相似,那么点查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com