
| A. | 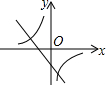 | B. | 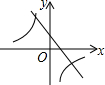 | C. | 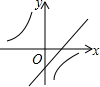 | D. | 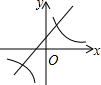 |
分析 根据一次函数和反比例函数的图象的性质分别判断后即可确定正确的选项.
解答 解:A、反比例函数的图象位于二、四象限,则k>0,得到直线应该交y轴的正半轴,错误;
B、反比例函数的图象位于二、四象限,则k>0,得到直线应该交y轴的负半轴,正确;
C、反比例函数的图象位于二、四象限,则k>0,得到直线应该呈下降趋势,错误;
D、反比例函数的图象位于一、三象限,则k<0,得到直线应该交y轴的负半轴,错误;
故选B.
点评 本题考查了反比例函数与一次函数的交点问题,属于基础题,主要理解一次函数和反比例函数y=$\frac{k}{x}$中k的几何意义.这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.


科目:初中数学 来源: 题型:解答题
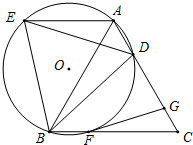 如图,△ABC是等边三角形,边长为6,D是AC边上一点,连接BD,⊙O为△ABD的外接圆,过点A作AE∥BC交⊙O于点E,连接DE、BE.
如图,△ABC是等边三角形,边长为6,D是AC边上一点,连接BD,⊙O为△ABD的外接圆,过点A作AE∥BC交⊙O于点E,连接DE、BE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
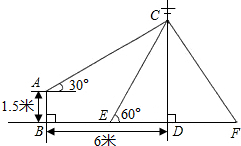 如图,在电线杆上的C处引拉线CE,CF固定电线杆,拉线CE和地面成60°角,在离电线杆6米的B是安置测角仪,在A处测得电线杆上C处的仰角为30°,已知测角仪AB的高为1.5米,求拉线CE的长($\sqrt{3}$≈1.73,结果精确到0.1米)
如图,在电线杆上的C处引拉线CE,CF固定电线杆,拉线CE和地面成60°角,在离电线杆6米的B是安置测角仪,在A处测得电线杆上C处的仰角为30°,已知测角仪AB的高为1.5米,求拉线CE的长($\sqrt{3}$≈1.73,结果精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
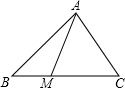 如图,在△ABC中,点M在边BC上,MC=2BM,设向量$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AM}$=$\overrightarrow{b}$,那么向量$\overrightarrow{BC}$=3$\overrightarrow{b}$-3$\overrightarrow{a}$(结果用$\overrightarrow{a}$、$\overrightarrow{b}$表示).
如图,在△ABC中,点M在边BC上,MC=2BM,设向量$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AM}$=$\overrightarrow{b}$,那么向量$\overrightarrow{BC}$=3$\overrightarrow{b}$-3$\overrightarrow{a}$(结果用$\overrightarrow{a}$、$\overrightarrow{b}$表示).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com