
【题目】如图,CD是⊙O的直径,且CD=2cm,点P为CD的延长线上一点,过点P作⊙O的切线PA,PB,切点分别为点A,B. 
(1)连接AC,若∠APO=30°,试证明△ACP是等腰三角形;
(2)填空: ①当DP=cm时,四边形AOBD是菱形;
②当DP=cm时,四边形AOBP是正方形.
【答案】
(1)解:连接OA,AC
∵PA是⊙O的切线,
∴OA⊥PA,
在Rt△AOP中,∠AOP=90°﹣∠APO=90°﹣30°=60°,
∴∠ACP=30°,
∵∠APO=30°
∴∠ACP=∠APO,
∴AC=AP,
∴△ACP是等腰三角形

(2)1;![]()
【解析】解:(2) ①DP=1,理由如下:
∵四边形AOBD是菱形,
∴OA=AD=OD,
∴∠AOP=60°,
∴OP=2OA,DP=OD.
∴DP=1,
②DP= ![]() ,理由如下:
,理由如下:
∵四边形AOBP是正方形,
∴∠AOP=45°,
∵OA=PA=1,OP= ![]() ,
,
∴DP=OP﹣1
∴DP= ![]() .
.
(1)利用切线的性质可得OC⊥PC.利用同弧所对的圆周角等于圆心角的一半,求得∠ACP=30°,从而求得.(2)①要使四边形AOBD是菱形,则OA=AD=OD,所以∠AOP=60°,所以OP=2OA,DP=OD.②要使四边形AOBP是正方形,则必须∠AOP=45°,OA=PA=1,则OP= ![]() ,所以DP=OP﹣1.
,所以DP=OP﹣1.


科目:初中数学 来源: 题型:
【题目】在读书月活动中,某校号召全体师生积极捐书,为了解所捐书籍的种类,图书管理员对部分书籍进行了抽样调查,根据调查数据绘制了如下不完整的统计图表.请你根据统计图表所提供的信息回答下面问题:
某校师生捐书种类情况统计表
种类 | 频数 | 百分比 |
A.科普类 | 12 | n |
B.文学类 | 14 | 35% |
C.艺术类 | m | 20% |
D.其它类 | 6 | 15% |
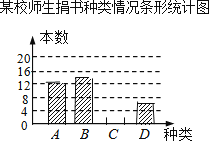
(1)统计表中的m= , n=;
(2)补全条形统计图;
(3)本次活动师生共捐书2000本,请估计有多少本科普类图书?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,
,![]() ,
,![]() ,
,![]() 都是正三角形,边长分别为2,
都是正三角形,边长分别为2,![]() ,
,![]() ,
,![]() ,且BO,
,且BO,![]() ,
,![]() ,
,![]() 都在x轴上,点A,
都在x轴上,点A,![]() ,
,![]() ,
,![]() 从左至右依次排列在x轴上方,若点
从左至右依次排列在x轴上方,若点![]() 是BO中点,点
是BO中点,点![]() 是
是![]() 中点,
中点,![]() ,且B为
,且B为![]() ,则点
,则点![]() 的坐标是
的坐标是![]()
![]()

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC和△ADE是等腰直角三角形,∠ACB=∠ADE=90°,点F为BE中点,连接DF、CF. 
(1)如图1,当点D在AB上,点E在AC上,请直接写出此时线段DF、CF的数量关系和位置关系(不用证明);
(2)如图2,在(1)的条件下将△ADE绕点A顺时针旋转45°时,请你判断此时(1)中的结论是否仍然成立,并证明你的判断;
(3)如图3,在(1)的条件下将△ADE绕点A顺时针旋转90°时,若AD=1,AC= ![]() ,求此时线段CF的长(直接写出结果).
,求此时线段CF的长(直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,∠C=30°,AC=12cm,点E从点A出发沿AB以每秒lcm的速度向点B运动,同时点D从点C出发沿CA以每秒2cm的速度向点A运动,运动时间为t秒(0<t<6),过点D作DF⊥BC于点F.
(I)试用含t的式子表示AE、AD、DF的长;
(Ⅱ)如图①,连接EF,求证:四边形AEFD是平行四边形;
(Ⅲ)如图②,连接DE,当t为何值时,四边形EBFD是矩形?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形OABC中,BC∥AO,∠AOC=90°,点A,B的坐标分别为(5,0),(2,6),点D为AB上一点,且BD=2AD,双曲线y= ![]() (k>0)经过点D,交BC于点E.
(k>0)经过点D,交BC于点E.
(1)求双曲线的解析式;
(2)求四边形ODBE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,直线l分别交x轴、y轴于A、B两点,AB=5,OA:OB =3:4.
(1)求直线l的表达式;
(2)点P是![]() 轴上的点,点Q是第一象限内的点.若以A、B、P、Q为顶点的四边形是菱形,请直接写出Q点的坐标.
轴上的点,点Q是第一象限内的点.若以A、B、P、Q为顶点的四边形是菱形,请直接写出Q点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】5月31日是世界无烟日.某市卫生机构为了了解“导致吸烟人口比例高的最主要原因”,随机抽样调查了该市部分18﹣65岁的市民.如图是根据调查结果绘制的统计图,根据图中信息解答下列问题: 
(1)这次接受随机抽样调查的市民总人数为;
(2)图1中的m的值是;
(3)求图2中认为“烟民戒烟的毅力弱”所对应的圆心角的度数;
(4)若该市18﹣65岁的市民约有200万人,请你估算其中认为导致吸烟人口比例高的最主要的原因是“对吸烟危害健康认识不足”的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com