
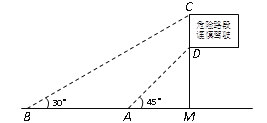
【题目】如图,为了测量矗立在高速公路水平地面上的交通警示牌的高度CD,在距M相距4米的A处,测得警示牌下端D的仰角为45°,再笔直往前走8米到达B处,在B处测得警示牌上端C的仰角为30°,求警示牌的高度CD.(结果精确到0.1米,参考数据:![]() ,
,![]() )
)
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠A=36°,AB的中垂线DE交AC于D,交AB于E,下述结论:(1)BD平分∠ABC;(2)AD=BD=BC;(3)△BDC的周长等于AB+BC;(4)D是AC中点.其中正确的命题序号是 . 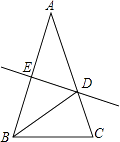
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】生物科技发展公司投资2000万元,研制出一种绿色保健食品.已知该产品的成本为40元/件,试销时,售价不低于成本价,又不高于180元/件.经市场调查知,年销售量y(万件)与销售单价![]() (元/件)的关系满足下表所示的规律.
(元/件)的关系满足下表所示的规律.

(1)y与![]() 之间的函数关系式是____________,自变量
之间的函数关系式是____________,自变量![]() 的取值范围为__________;
的取值范围为__________;
(2)经测算:年销售量不低于90万件时,每件产品成本降低2元,设销售该产品年获利润为![]() (万元)(
(万元)( ![]() 年销售额一成本一投资),求出年销售量低于90万件和不低于90万件时,
年销售额一成本一投资),求出年销售量低于90万件和不低于90万件时, ![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)在(2)的条件下,当销售单价定为多少时,公司销售这种产品年获利润最大?最大利润为多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
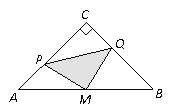
【题目】如图,在△ABC中,∠C=90°,AC=BC=4cm,M是AB的中点,点P、Q分别从A、C两点同时出发,以1cm/s的速度沿AC、CB方向均速运动,到点C、B时停止运动,设运动时间为![]() ,△PMQ的面积为S (cm2),则S (cm2)与
,△PMQ的面积为S (cm2),则S (cm2)与![]() 的函数关系可用图象表示为( )
的函数关系可用图象表示为( )
A.  B.
B. 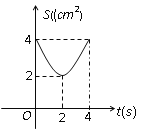 C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】去年入秋以来,某省发生了百年一遇的旱灾,连续8个多月无有效降水,为抗旱救灾,某部队计划为驻地村民新修水渠3600米,为了水渠能尽快投入使用,实际工作效率是原计划工作效率的1.8倍,结果提前20天完成修水渠任务.问原计划每天修水渠多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
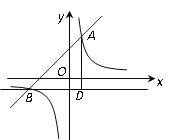
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点A(1,3)和B(-3,
的图象交于点A(1,3)和B(-3, ![]() ).
).
(1)求一次函数和反比例函数的解析式;
(2)点C是平面直角坐标系内一点,BC∥![]() 轴,AD⊥BC于点D,连结AC,若
轴,AD⊥BC于点D,连结AC,若![]() ,求点C的坐标.
,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,∠BOC=80°,OE是∠BOC的角平分线,OF是OE的反向延长线.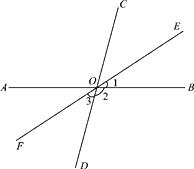
(1)求∠2、∠3的度数;
(2)说明OF平分∠AOD的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为深化义务教育课程改革,满足学生的个性化学习需求,某校就“学生对知识拓展,体育特长、艺术特长和实践活动四类选课意向”进行了抽样调查(每人选报一类),绘制了如图所示的两幅统计图(不完整),请根据图中信息,解答下列问题:

(1)扇形统计图中m的值为 ,n的值为 ;
(2)补全条形统计图;
(3)在选择B类的学生中,甲、乙、丙三人在乒乓球项目表现突出,现决定从这三名同学中任选两名参加市里组织的乒乓球比赛,选中甲同学的概率是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com