
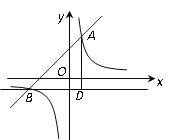
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点A(1,3)和B(-3,
的图象交于点A(1,3)和B(-3, ![]() ).
).
(1)求一次函数和反比例函数的解析式;
(2)点C是平面直角坐标系内一点,BC∥![]() 轴,AD⊥BC于点D,连结AC,若
轴,AD⊥BC于点D,连结AC,若![]() ,求点C的坐标.
,求点C的坐标.
【答案】(1)反比例函数解析式为![]() ,一次函数解析式为
,一次函数解析式为![]() .(2)点C的坐标为C(-1,-1)或(3,-1).
.(2)点C的坐标为C(-1,-1)或(3,-1).
【解析】试题分析:(1)将点A坐标代入反比例函数![]() 中,得出k的值,再求出m的值,将A、B两点坐标代入一次函数中,求出a、b的值即可;(2)设点C的横坐标为x,
中,得出k的值,再求出m的值,将A、B两点坐标代入一次函数中,求出a、b的值即可;(2)设点C的横坐标为x,
根据点A(1,3)、B(-3,-1)得出CD、AD的长度,在Rt△ACD中,根据CD2+AD2=AC2,即可求出x的值,即可得点C的坐标;
试题解析:
(1)将点A(1,3)代入反比例函数解析式![]() 得,
得,
![]() ,
,
∴反比例函数解析式为![]() ,
,

∵A(1,3)和B(-3, ![]() )都在反比例函数的图象上,
)都在反比例函数的图象上,
∴![]() ,
,
解得: ![]() ,
,
∴B(-3,-1),
∵一次函数![]() 的图象经过A(1,3)和B(-3,-1),
的图象经过A(1,3)和B(-3,-1),
∴![]() ,
,
解得: ![]() ,
,
∴一次函数解析式为![]() .
.
(2)∵BC∥![]() 轴,AD⊥BC于点D,且A(1,3),B(-3,-1),设点C的横坐标为x,
轴,AD⊥BC于点D,且A(1,3),B(-3,-1),设点C的横坐标为x,
∴D(1,-1),C(![]() ,-1),
,-1),
∴![]() ,AD=4,
,AD=4,
∵![]() ,
,
∴在Rt△ACD中,有![]() ,
,
解得: ![]() ,
, ![]() ,
,
∴点C的坐标为C(-1,-1)或(3,-1).


科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过坐标原点O和x轴上另一点E,顶点M的坐标为(2,4);矩形ABCD的顶点A与点O重合,AD、AB分别在x轴、y轴上,且AD=2,AB=3.
(1)求该抛物线所对应的函数关系式;
(2)将矩形ABCD以每秒1个单位长度的速度从如图所示的位置沿x轴的正方向匀速平行移动,同时一动点P也以相同的速度从点A出发向B匀速移动,设它们运动的时间为t秒(0≤t≤3),直线AB与该抛物线的交点为N(如图2所示).
①当t=![]() 时,判断点P是否在直线ME上,并说明理由;
时,判断点P是否在直线ME上,并说明理由;
②设以P、N、C、D为顶点的多边形面积为S,试问S是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
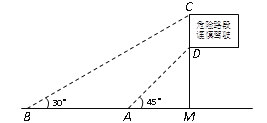
【题目】如图,为了测量矗立在高速公路水平地面上的交通警示牌的高度CD,在距M相距4米的A处,测得警示牌下端D的仰角为45°,再笔直往前走8米到达B处,在B处测得警示牌上端C的仰角为30°,求警示牌的高度CD.(结果精确到0.1米,参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】荔枝是岭南一带的特色时令水果.今年5月份荔枝一上市,某水果店的老板用3000元购进了一批荔枝,由于荔枝刚在果园采摘比较新鲜,前两天他以高于进价40% 的价格共卖出150千克,由于荔枝保鲜期短,第三天他发现店里的荔枝卖相已不大好,于是果断地将剩余荔枝以低于进价20%的价格全部售出,前后一共获利750元.
(1)若购进的荔枝为![]() 千克,则这批荔枝的进货价为 ;(用含
千克,则这批荔枝的进货价为 ;(用含![]() 的式子来表示)
的式子来表示)
(2)求该水果店的老板这次购进荔枝多少千克.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com