
【题目】如图,已知抛物线经过坐标原点O和x轴上另一点E,顶点M的坐标为(2,4);矩形ABCD的顶点A与点O重合,AD、AB分别在x轴、y轴上,且AD=2,AB=3.
(1)求该抛物线所对应的函数关系式;
(2)将矩形ABCD以每秒1个单位长度的速度从如图所示的位置沿x轴的正方向匀速平行移动,同时一动点P也以相同的速度从点A出发向B匀速移动,设它们运动的时间为t秒(0≤t≤3),直线AB与该抛物线的交点为N(如图2所示).
①当t=![]() 时,判断点P是否在直线ME上,并说明理由;
时,判断点P是否在直线ME上,并说明理由;
②设以P、N、C、D为顶点的多边形面积为S,试问S是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.

【答案】(1)![]() ;(2)①不在;②最大值为
;(2)①不在;②最大值为![]() .
.
【解析】
试题分析:(1)已知顶点坐标,又抛物线经过原点,用待定系数可求出抛物线解析式;
(2)①根据抛物线的对称性求出E点坐标,再求出直线ME的解析式,把t知代入验证点P是否在直线ME上;
②最后一问设出P,N坐标,根据几何关系求出PN,然后分两种情况讨论:(1)PN=0;(2)PN≠0;把求多边形面积S转化为求函数最值问题.
试题解析:(1)因所求抛物线的顶点M的坐标为(2,4),故可设其关系式为![]() ,又∵抛物线经过O(0,0),∴得
,又∵抛物线经过O(0,0),∴得![]() ,解得a=﹣1,∴所求函数关系式为
,解得a=﹣1,∴所求函数关系式为![]() ,即
,即![]() .
.
(2)①点P不在直线ME上.根据抛物线的对称性可知E点的坐标为(4,0),又M的坐标为(2,4),设直线ME的关系式为y=kx+b.于是得:![]() ,解得:
,解得:![]() ,所以直线ME的关系式为y=﹣2x+8.
,所以直线ME的关系式为y=﹣2x+8.
由已知条件易得,当t=![]() 时,OA=AP=
时,OA=AP=![]() ,∴P(
,∴P(![]() ,
,![]() ).
).
∵P点的坐标不满足直线ME的关系式y=﹣2x+8,∴当t=![]() 时,点P不在直线ME上.
时,点P不在直线ME上.
②S存在最大值.理由如下:
∵点A在x轴的非负半轴上,且N在抛物线上,∴OA=AP=t,∴点P,N的坐标分别为(t,t)、(t,![]() ),∴AN=
),∴AN=![]() (0≤t≤3),∴AN﹣AP=(
(0≤t≤3),∴AN﹣AP=(![]() )﹣t=
)﹣t=![]() =t(3﹣t)≥0,∴PN=
=t(3﹣t)≥0,∴PN=![]() .(ⅰ)当PN=0,即t=0或t=3时,以点P,N,C,D为顶点的多边形是三角形,此三角形的高为AD,∴S=
.(ⅰ)当PN=0,即t=0或t=3时,以点P,N,C,D为顶点的多边形是三角形,此三角形的高为AD,∴S=![]() DCAD=
DCAD=![]() ×3×2=3.
×3×2=3.
(ⅱ)当PN≠0时,以点P,N,C,D为顶点的多边形是四边形.
∵PN∥CD,AD⊥CD,∴S=![]() (CD+PN)AD=
(CD+PN)AD=![]() =
=![]() =
=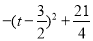 ,其中(0<t<3),由a=﹣1,0<
,其中(0<t<3),由a=﹣1,0<![]() <3,此时S最大=
<3,此时S最大=![]() .
.
综上所述,当t=![]() 时,以点P,N,C,D为顶点的多边形面积有最大值,这个最大值为
时,以点P,N,C,D为顶点的多边形面积有最大值,这个最大值为![]() .
.
说明:(ⅱ)中的关系式,当t=0和t=3时也适合.


 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:
【题目】下表是篮球运动员在一些篮球比赛中罚球的记录:
罚球数 | 4 | 5 | 6 | 3 | 3 | 5 |
罚中球数 | 3 | 4 | 5 | 2 | 3 | 3 |
(1)计算表中“罚中频率不低于0.8”的有几次;
(2)根据这些罚球频率,估计该运动员的罚中球概率(精确0.01)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段AB,点C是它的黄金分割点(AC>BC)设以AC为边的正方形的面积为S1,以AB、CB分别为长和宽的矩形的面积为S2,则S1与S2关系正确的是( )
A.S1>S2B.S1=S2C.S1<S2D.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠A=36°,AB的中垂线DE交AC于D,交AB于E,下述结论:(1)BD平分∠ABC;(2)AD=BD=BC;(3)△BDC的周长等于AB+BC;(4)D是AC中点.其中正确的命题序号是 . 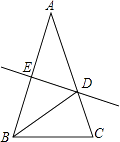
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察图形,解答问题:
(1)按下表已填写的形式填写表中的空格:
图① | 图② | 图③ | |
三个角上三个数的积 | 1×(﹣1)×2=﹣2 | (﹣3)×(﹣4)×(﹣5)=﹣60 | |
三个角上三个数的和 | 1+(﹣1)+2=2 | (﹣3)+(﹣4)+(﹣5)=﹣12 | |
积与和的商 | ﹣2÷2=﹣1 |
(2)请用你发现的规律求出图④中的数y和图⑤中的数x.
查看答案和解析>>
科目:初中数学 来源: 题型:
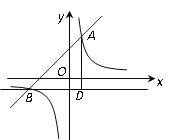
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点A(1,3)和B(-3,
的图象交于点A(1,3)和B(-3, ![]() ).
).
(1)求一次函数和反比例函数的解析式;
(2)点C是平面直角坐标系内一点,BC∥![]() 轴,AD⊥BC于点D,连结AC,若
轴,AD⊥BC于点D,连结AC,若![]() ,求点C的坐标.
,求点C的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com