

分析 (1)根据三角形内角和定理推知∠A=30,∠C=90°.
(2)根据线段垂直平分线的性质知CD=BD,则△ACD的周长等于AC+AB;
(3)如图3,连接AD.利用等腰三角形的性质、垂直的定义推知∠B=∠ADE=30°,然后由”30度角所对的直角边是斜边的一半“分别求得BE、AE的值;
(4)如图4,连接AD,由DM是AB的垂直平分线,得到AD=BD=8cm,根据外角的性质得到∠ADC=30°,根据直角三角形的性质得到结论;
(5)如图5,根据全等三角形的判定定理SAS可判断两个三角形全等;根据全等三角形的对应角相等,以及三角形外角的性质,可以得到∠PBQ=30°,根据直角三角形的性质即可得到.
解答 解:(1)∵∠A:∠B:∠C=1:2:3,且∠A+∠B+∠C=180°,
∴∠A=30,∠C=90°,
∴BC=$\frac{1}{2}$AB=$\frac{a}{2}$.
故答案为:$\frac{a}{2}$;
(2)如图2,∵DE是线段BC的垂直平分线,∠ACB=90°,
∴CD=BD,AD=BD.
又∵在△ABC中,∠ACB=90°,∠B=30°,
∴AC=$\frac{1}{2}$AB,
∴△ACD的周长=AC+AB=3BD=15cm.
故答案为:15cm;
(3)如图3,连接AD.
∵在△ABC中,AB=AC,∠A=120°,D是BC的中点,
∴∠BAD=60°.
又∵DE⊥AB,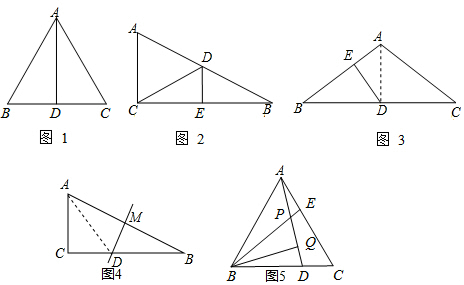
∴∠B=∠ADE=30°,
∴BE=$\frac{\sqrt{3}}{2}$BD,AE=$\frac{1}{2}$AD,
∴BE:EA=$\frac{\sqrt{3}}{2}$BD:$\frac{1}{2}$AD,
又∵BD=$\sqrt{3}$AD,
∴BE:AE=3:1.
故答案为:3:1;
(4)如图4,连接AD,
∵DM是AB的垂直平分线,
∴AD=BD=8cm,
∴∠DAB=∠B=15°,
∴∠ADC=30°,
∴AC=$\frac{1}{2}$AD=4cm,
故答案为:4cm;
(5))BP=2PQ.理由如下:
∵△ABC为等边三角形.
∴AB=AC,∠BAC=∠ACB=60°,
在△BAE和△ACD中,$\left\{\begin{array}{l}{AE=CD}\\{∠BAC=∠ACB}\\{AB=AC}\end{array}\right.$,
∴△BAE≌△ACD(SAS),
∴∠ABE=∠CAD.
∵∠BPQ为△ABP外角,
∴∠BPQ=∠ABE+∠BAD.
∴∠BPQ=∠CAD+∠BAD=∠BAC=60°
∵BQ⊥AD,
∴∠PBQ=30°,
∴BP=2PQ.
点评 本题考查了等腰三角形的性质、等边三角形的性质以及含30度角直角三角形的性质.直角三角形中30°的锐角所对的直角边等于斜边的一半.


科目:初中数学 来源: 题型:解答题
 在比赛中,某次羽毛球的运动路线可以看作是抛物线y=-$\frac{1}{4}$x2+bx+c的一部分,如图,其中出球点B离地面O点的距离是1m,球落地点A到O点的距离是4m,求这条抛物线的解析式和羽毛球飞行的最大高度.
在比赛中,某次羽毛球的运动路线可以看作是抛物线y=-$\frac{1}{4}$x2+bx+c的一部分,如图,其中出球点B离地面O点的距离是1m,球落地点A到O点的距离是4m,求这条抛物线的解析式和羽毛球飞行的最大高度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,把长方形纸片ABCD沿EF折叠后,点D与点B重合,点C落在点C'的位置上,若∠1=60°,AE=1.
已知:如图,把长方形纸片ABCD沿EF折叠后,点D与点B重合,点C落在点C'的位置上,若∠1=60°,AE=1.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
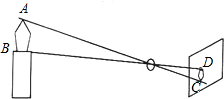 如图,火焰的光线穿过小孔O,在竖直的屏幕上形成倒立的实像,如果$\frac{OA}{OC}$=$\frac{OB}{OD}$=n,像的高度为CD=b,则火焰的高度是nb.
如图,火焰的光线穿过小孔O,在竖直的屏幕上形成倒立的实像,如果$\frac{OA}{OC}$=$\frac{OB}{OD}$=n,像的高度为CD=b,则火焰的高度是nb.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 车序号 | 1 | 2 | 3 | 4 | 5 | 6 |
| 车速(千米/时) | 66 | 56 | 71 | 54 | 69 | 58 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,如果△ABC沿直线MN折叠后,与△A'B'C完全重合,我们就说△ABC与△A'B'C'关于直线MN对称;直线MN是对称轴;点A与点A'叫做对称点,图中还有类似的点是点B与点B',点C与点C',图中还有相等的线段和角,分别为AB=A'B'、AC=A'C、BC=B'C;∠A=∠A'、∠B=∠B'、∠C=∠C'.
如图,如果△ABC沿直线MN折叠后,与△A'B'C完全重合,我们就说△ABC与△A'B'C'关于直线MN对称;直线MN是对称轴;点A与点A'叫做对称点,图中还有类似的点是点B与点B',点C与点C',图中还有相等的线段和角,分别为AB=A'B'、AC=A'C、BC=B'C;∠A=∠A'、∠B=∠B'、∠C=∠C'.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com