
【题目】如图在□ABCD,∠ABC的平分线交AD于点E,延长BE交CD的延长线于F.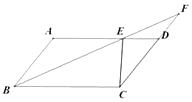
(1)若∠F=20°,求∠A的度数;
(2)若AB=5,BC=8,CE⊥AD,求□ABCD的面积;
【答案】
(1)
解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC=8,CD=AB=5,AB∥CD,
∴∠AEB=∠CBF,∠ABE=∠F=20°,
∵∠ABC的平分线交AD于点E,
∴∠ABE=∠CBF,
∴∠AEB=∠ABE=20°,
∴AE=AB,∠A=(180°-20°-20°)÷2=140°;
(2)
∵AE=AB=5,AD=BC=8,CD=AB=5,
∴DE=AD-AE=3,
∵CE⊥AD,
∴CE= ![]()
=4,
∴ABCD的面积=ADCE=8×4=32.
【解析】(1)由平行四边形的性质和已知条件得出∠AEB=∠CBF,∠ABE=∠F=20°,证出∠AEB=∠ABE=20°,由三角形内角和定理求出结果即可;(2)求出DE,由勾股定理求出CE,即可得出结果.
【考点精析】掌握三角形的内角和外角和勾股定理的概念是解答本题的根本,需要知道三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


科目:初中数学 来源: 题型:
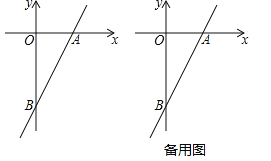
【题目】已知一次函数![]() 的图象与x轴、y轴分别相交于点A、B,点P在该函数的图象上,P到x轴、y轴的距离分别为
的图象与x轴、y轴分别相交于点A、B,点P在该函数的图象上,P到x轴、y轴的距离分别为![]() 、
、![]() .
.
(1)当P为线段AB的中点时,求![]() 的值;
的值;
(2)直接写出![]() 的范围,并求当
的范围,并求当![]() 时点P的坐标;
时点P的坐标;
(3)若在线段AB上存在无数个P点,使![]() (a为常数),求a的值.
(a为常数),求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;其中正确结论的为(请将所有正确的序号都填上).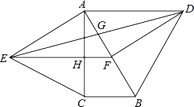
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算。
(1)你发现了吗?( ![]() )2=
)2= ![]() ×
× ![]() ,(
,( ![]() )﹣2=
)﹣2= ![]() =
= ![]() ×
× ![]() =
= ![]() ×
× ![]() 由上述计算,我们发现(
由上述计算,我们发现( ![]() )2(
)2( ![]() )﹣2;
)﹣2;
(2)仿照(1),请你通过计算,判断( ![]() )3与(
)3与( ![]() )﹣3之间的关系.
)﹣3之间的关系.
(3)我们可以发现:( ![]() )﹣m(
)﹣m( ![]() )m(ab≠0)
)m(ab≠0)
(4)计算:( ![]() )﹣4×(
)﹣4×( ![]() )4 .
)4 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图中的折线ABC表示某汽车的耗油量y(单位:L/km)与速度x(单位:km/h)之间的函数关系(30≤x≤120),已知线段BC表示的函数关系中,该汽车的速度每增加1km/h,耗油量增加0.002L/km.
(1)当速度为50km/h、100km/h时,该汽车的耗油量分别为 L/km、 L/km.
(2)求线段AB所表示的y与x之间的函数表达式.
(3)速度是多少时,该汽车的耗油量最低?最低是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
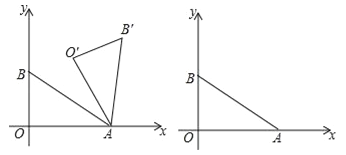
【题目】如图,在平面直角坐标系xOy中,一次函数![]() 的图象与x轴、y轴分别交于点A、B,把Rt△AOB绕点A顺时针旋转角α(30°<α<180°),得到△AO′B′.
的图象与x轴、y轴分别交于点A、B,把Rt△AOB绕点A顺时针旋转角α(30°<α<180°),得到△AO′B′.
(1)当α=60°时,判断点B是否在直线O′B′上,并说明理由;
(2)连接OO′,设OO′与AB交于点D,当α为何值时,四边形ADO′B′是平行四边形?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com