
【题目】如图,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8.在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求(1)求直线AE的函数表达式;(2)求D点的坐标.

【答案】(1)![]() ;(2)D(0,5).
;(2)D(0,5).
【解析】
(1)先根据勾股定理求出BE的长,进而可得出CE的长,求出E点坐标,根据点A、E的坐标即可求直线AE的函数表达式;
(2)在Rt△DCE中,由DE=OD及勾股定理可求出OD的长,进而得出D点坐标.
解:(1)∵将矩形纸片沿AD翻折,使点O落在BC边上的点E处,
∴在Rt△ABE中,AE=AO=10,AB=8,BE=![]() =
=![]() =6,
=6,
∴CE=BC-BE=10-6=4,
∴E(4,8),
∵点A在x轴的正半轴上,OA=10,
∴A(10,0),
设直线AE的函数表达式为y=kx+b,
则![]() ,解得:
,解得: ,
,
∴直线AE的函数表达式为:![]() ;
;
(2)在Rt△DCE中,DC2+CE2=DE2,
∵DE=OD,CD=8-OD,
∴(8-OD)2+42=OD2,
解得:OD=5,
∴D(0,5).


科目:初中数学 来源: 题型:
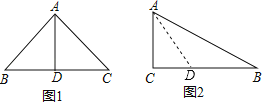
【题目】定义:如果经过三角形一个顶点的线段把这个三角形分成两个小三角形,其中一个三角形是等腰三角形,另外一个三角形和原三角形的三个内角分别相等,那么这条线段称为原三角形的“和谐分割线”,例如:如图1,等腰直角三角形斜边上的中线就是一条“和谐分割线”.
(1)判断(对的打“√”,错的打“×”)
①等边三角形存在“和谐分割线”( )
②如果三角形中有一个角是另一个角的两倍,则这个三角形必存在“和谐分割线”( )
(2)如图2,Rt△ABC,∠C=90°,∠B=30°,BC=6,请用尺规画出“和谐分割线”,并计算“和谐分割线”的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形ABC中,D、E分别是AB、AC的中点,延长BC至点F,使CF =![]() BC,连接DE、CD、EF.
BC,连接DE、CD、EF.

(1)求证:四边形DCFE是平行四边形;
(2)若等边三角形ABC的边长为a,写出求EF长的思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD⊥BC,垂足为D,AD=4,BD=2,CD=8.

(1)求证:∠BAC=90°;
(2)P为BC边上一点,连接AP,若△ABP为等腰三角形,请求出BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.
(1)求证:△ABE≌△ACD;
(2)求证:DC⊥BE.

查看答案和解析>>
科目:初中数学 来源: 题型:
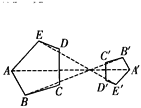
【题目】如图,五边形ABCDE与五边形A'B'C'D'E'是位似图形,且位似比为2.如果五边形ABCDE的面积为16 cm2,周长为20 cm,那么五边形A'B'C'D'E'的面积为_______,周长为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是小李骑自行车离家的距离![]() 与时间
与时间![]() 之间的关系.
之间的关系.
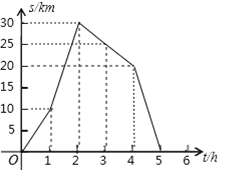
(1)在这个变化过程中自变量是______,因变量是______;
(2)小李何时到达离家最远的地方?此时离家多远?
(3)请直接写出小李何时与家相距![]() ?
?
(4)求出小李这次出行的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8.在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D,E两点的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com