
【题目】如图,某地方政府决定在相距50km的A、B两站之间的公路旁E点,修建一个土特产加工基地,且使C、D两村到E点的距离相等,已知DA⊥AB于A,CB⊥AB于B,DA=30km,CB=20km,那么基地E应建在离A站多少千米的地方?
【答案】解:设基地E应建在离A站x千米的地方.
则BE=(50﹣x)千米
在Rt△ADE中,根据勾股定理得:AD2+AE2=DE2
∴302+x2=DE2
在Rt△CBE中,根据勾股定理得:CB2+BE2=CE2
∴202+(50﹣x)2=CE2
又∵C、D两村到E点的距离相等.
∴DE=CE∴DE2=CE2
∴302+x2=202+(50﹣x)2
解得x=20
∴基地E应建在离A站多少20千米的地方
【解析】设基地E应建在离A站x千米的地方.根据题意表示出BE的长,再在Rt△ADE中和Rt△CBE中,利用勾股定理表示出DE2和CE2 , 然后根据C、D两村到E点的距离相等.得出DE2=CE2 , 建立方程,解方程求解即可。


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等三角形的对数是( ) 
A.1对
B.2对
C.3对
D.4对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB>BC,AB=AC,DE是AB的垂直平分线,垂足为D,交AC于E. 
(1)若∠ABE=45°,求∠EBC的度数;
(2)若AB+BC=30,求△BCE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(操作发现)
在计算器上输入一个正数,不断地按“![]() ”键求算术平方根,运算结果越来越接近1或都等于1.
”键求算术平方根,运算结果越来越接近1或都等于1.
【提出问题】
输入一个实数,不断地进行“乘以常数k,再加上常数b”的运算,有什么规律?
【分析问题】
我们可用框图表示这种运算过程(如图a).
也可用图象描述:如图1,在x轴上表示出x1,先在直线y=kx+b上确定点(x1,y1),再在直线y=x上确定纵坐标为y1的点(x2,y1),然后再x轴上确定对应的数x2,…,以此类推.
【解决问题】
研究输入实数x1时,随着运算次数n的不断增加,运算结果x,怎样变化.
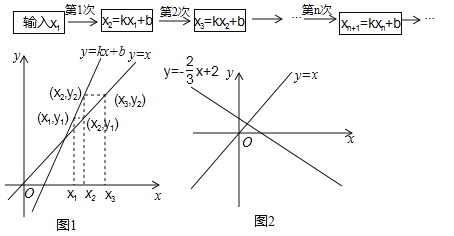
(1)若k=2,b=﹣4,得到什么结论?可以输入特殊的数如3,4,5进行观察研究;
(2)若k>1,又得到什么结论?请说明理由;
(3)①若![]() ,b=2,已在x轴上表示出x1(如图2所示),请在x轴上表示x2,x3,x4,并写出研究结论;
,b=2,已在x轴上表示出x1(如图2所示),请在x轴上表示x2,x3,x4,并写出研究结论;
②若输入实数x1时,运算结果xn互不相等,且越来越接近常数m,直接写出k的取值范围及m的值(用含k,b的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下面的变形规律:![]() =1﹣
=1﹣ ![]() ;
; ![]() =
= ![]() ﹣
﹣ ![]() ;
; ![]() =
= ![]() ﹣
﹣ ![]() ;…解答下面的问题:
;…解答下面的问题:
(1)若n为正整数,请你猜想 ![]() =;
=;
(2)求和: ![]() +
+ ![]() +
+ ![]() .(注:只能用上述结论做才能给分);
.(注:只能用上述结论做才能给分);
(3)用上述相似的方法求和: ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com