练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，矩形的对角线相交于点．

    (1)求证：四边形为菱形；

    (2)垂直平分线段于点，求的长．

    【答案】(1) 见解析；(2)

    【解析】

    （1）先根据平行四边形的定义判定四边形为平行四边形，然后由矩形的性质可得OD=OC，进一步即可证得结论；

    （2）根据线段垂直平分线的性质和矩形的性质可得是边长为6的等边三角形，进而可得△BOC是顶角为120°的等腰三角形，过作于点E，由30°的直角三角形的性质可求出OE的长，再根据勾股定理即可求出BE的长，进一步即得BC的长．

    （1）证明：，

    四边形是平行四边形，

    矩形的对角线相交于点，

    ∴AO=CO，BO=DO，AC=BD，

    ，

    平行四边形为菱形；

    （2）解：矩形的对角线相交于点，AC=12，

    ，

    垂直平分线段于点，

    ，

    ∴AB=AO=BO=6，

    是等边三角形，

    ．

    ．

    过作与点E，如图，则．

    ，

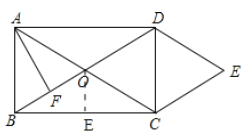
    ∵BO=6，∴，

    ．

    ∴．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

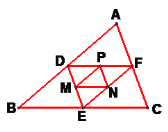
    【题目】如图，△ABC的周长为16，D， E，F分别为AB， BC，AC的中点，M，N，P分别为DE， EF，DF的中点，则△MNP的周长为____；如果△ABC，△DEF，△MNP分别为第1个，第2个，第3个三角形，按照上述方法继续做三角形，那么第n个三角形的周长是___．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某宾馆有50个房间供游客居住，当每个房间每天的定价为180元时，房间会全部住满；当每个房间每天的定价每增加10元时，就会有一个房间空闲．如果游客居住房间，宾馆需对每个房间每天支出20元的各种费用．

    （1）若每个房间定价增加40元，则这个宾馆这一天的利润为多少元？

    （2）若宾馆某一天获利10640元，则房价定为多少元？

    （3）房价定为多少时，宾馆的利润最大？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为加强中小学生安全和禁毒教育，某校组织了“防溺水、交通安全、禁毒”知识竞赛，为奖励在竞赛中表现优异的班级，学校准备从体育用品商场一次性购买若干个足球和篮球（每个足球的价格相同，每个篮球的价格相同），购买1个足球和1个篮球共需159元；足球单价是篮球单价的2倍少9元．

    （1）求足球和篮球的单价各是多少元？

    （2）根据学校实际情况，需一次性购买足球和篮球共20个，但要求购买足球和篮球的总费用不超过1550元，学校最多可以购买多少个足球？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，二次函数y=ax2+bx+c（a＞0）图象的顶点为D，其图象与x轴的交点A、B的横坐标分别为﹣1，3．与y轴负半轴交于点C，在下面五个结论中：

    ①2a﹣b=0；②c=﹣3a；③当m≠1时，a+b＜am2+bm；

    ④若ax12+bx1=ax22+bx2，且x1≠x2，则x1+x2=2；

    ⑤使△ACB为等腰三角形的a值可以有三个．其中正确的结论是_________．（只填序号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠ABC=90°，CD⊥BC，BD与AC相交于点E，AB=9，BC=4，DC=3．

    （1）求BE的长度；

    （2）求△ABE的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】先阅读下列一段文字，再解答问题：

    已知在平面内有两点，，其两点间的距离公式为；同时，当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时，两点间距离公式可简化为或.

    （1）已知点A（2，4），B（-2，1），则AB=__________；

    （2）已知点C，D在平行于y轴的直线上，点C的纵坐标为4，点D的纵坐标为-2，则CD=__________；

    （3）已知点P（3，1）和（1）中的点A，B，判断线段PA，PB，AB中哪两条线段的长是相等的？并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

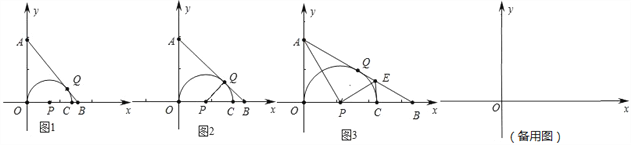
    【题目】平面直角坐标系中，A（0，4），点P从原点O开始向x轴正方向运动，设P点横坐标为m，以点P为圆心，PO为半径作⊙P交x 轴另一点为C，过点A作⊙P的切线交 x轴于点B，切点为Q．

    （1）如图1，当B点坐标为（3，0）时，求m；

    （2）如图2，当△PQB为等腰三角形时，求m；

    （3）如图3，连接AP，作PE⊥AP交AB于点E，连接CE，求证：CE是⊙P的切线；

    （4）若在x轴上存在点M（8，0），在点P整个运动过程中，求MQ的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图， 是的外接圆， 点在边上， 的平分线交于点，连接，过点作的平行线，与的延长线相交于点.

    （1）求证： 是的切线；

    （2）求证：△PBD∽△DCA；

    （3）当时，求线段的长.

    查看答案和解析>>

    同步练习册答案