
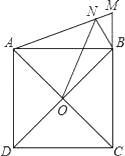
【题目】如图,正方形ABCD的边长为3,延长CB至点M,使S△ABM=![]() ,过点B作BN⊥AM,垂足为N,O是对角线AC,BD的交点,连接ON,则ON的长为________.
,过点B作BN⊥AM,垂足为N,O是对角线AC,BD的交点,连接ON,则ON的长为________.
【答案】![]()
【解析】
】先根据三角形的面积公式求出BM的长,由条件可证得△ABN∽△BNM∽△ABM,且可求得AM=![]() ,利用对应线段的比相等可求得AN和MN,进一步可得到
,利用对应线段的比相等可求得AN和MN,进一步可得到![]() =
=![]() ,且∠CAM=∠NAO,可证得△AON∽△AMC,利用相似三角形的性质可求得ON.
,且∠CAM=∠NAO,可证得△AON∽△AMC,利用相似三角形的性质可求得ON.
∵正方形ABCD的边长为3,S△ABM=![]() ,
,
∴BM=![]() ,
,
∵AB=3,BM=1,
∴AM=![]() ,
,
∵∠ABM=90°,BN⊥AM,
∴△ABN∽△BNM∽△AMB,
∴AB2=AN×AM,BM2=MN×AM,
∴AN=![]() ,MN=
,MN=![]() ,
,
∵AB=3,CD=3,
∴AC=3![]() ,
,
∴AO=![]() ,
,
∵![]() =
=![]() ,
,![]() =
=![]() ,
,
∴![]() =
=![]() ,且∠CAM=∠NAO,
,且∠CAM=∠NAO,
∴△AON∽△AMC,
∴![]() =
=![]() =
=![]() ,
,
∴ON=![]() .
.
故答案为:![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
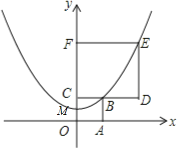
【题目】如图,正方形OABC和正方形CDEF在平面直角坐标系中,点O,C,F在y轴上,点O为坐标原点,点M为OC的中点,抛物线y=ax2+b经过M,B,E三点,则![]() 的值为 .
的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分9分)
根据要求,解答下列问题.
(1)根据要求,解答下列问题.
①方程x2-2x+1=0的解为________________________;
②方程x2-3x+2=0的解为________________________;
③方程x2-4x+3=0的解为________________________;
…… ……
(2)根据以上方程特征及其解的特征,请猜想:
①方程x2-9x+8=0的解为________________________;
②关于x的方程________________________的解为x1=1,x2=n.
(3)请用配方法解方程x2-9x+8=0,以验证猜想结论的正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,抛物线y=ax2+bx+c与坐标轴分别交于点A(0,6),B(6,0),C(﹣2,0),点P是线段AB上方抛物线上的一个动点.
(1)求抛物线的解析式;
(2)当点P运动到什么位置时,△PAB的面积有最大值?
(3)过点P作x轴的垂线,交线段AB于点D,再过点P做PE∥x轴交抛物线于点E,连结DE,请问是否存在点P使△PDE为等腰直角三角形?若存在,求出点P的坐标;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学对本校500名毕业生中考体育加试测试情况进行调查,根据男生1 000m及女生800m测试成绩整理、绘制成如下不完整的统计图(图①、图②),请根据统计图提供的信息,回答下列问题:
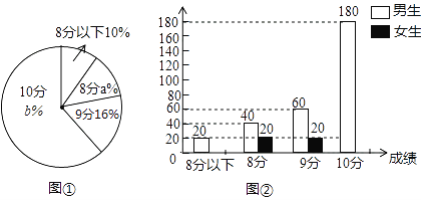
(1)该校毕业生中男生有________人,女生有________人;
(2)扇形统计图中a=________,b=________;
(3)补全条形统计图(不必写出计算过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明准备测量一段水渠的深度,他把一根竹竿AB竖直插到水底,此时竹竿AB离岸边点C处的距离![]() 米。竹竿高出水面的部分AD长0.5米,如果把竹竿的顶端A拉向岸边点C处,竿顶和岸边的水面刚好相齐,则水渠的深度BD为( )
米。竹竿高出水面的部分AD长0.5米,如果把竹竿的顶端A拉向岸边点C处,竿顶和岸边的水面刚好相齐,则水渠的深度BD为( )
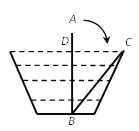
A. 2米B. 2.5米C. 2.25米D. 3米
查看答案和解析>>
科目:初中数学 来源: 题型:
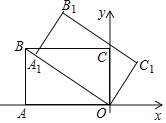
【题目】如图,平面直角坐标系中,矩形OABC的顶点A(﹣6,0),C(0,2![]() ).将矩形OABC绕点O顺时针方向旋转,使点A恰好落在OB上的点A1处,则点B的对应点B1的坐标为_____.
).将矩形OABC绕点O顺时针方向旋转,使点A恰好落在OB上的点A1处,则点B的对应点B1的坐标为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com