
【题目】某中学对本校500名毕业生中考体育加试测试情况进行调查,根据男生1 000m及女生800m测试成绩整理、绘制成如下不完整的统计图(图①、图②),请根据统计图提供的信息,回答下列问题:
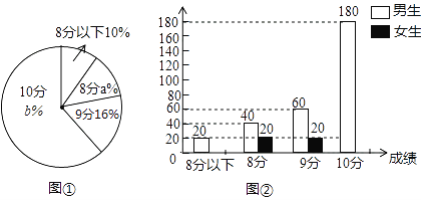
(1)该校毕业生中男生有________人,女生有________人;
(2)扇形统计图中a=________,b=________;
(3)补全条形统计图(不必写出计算过程).
【答案】(1)300;200(2)12;62;(3)见解析.
【解析】
(1)男生人数为20+40+60+180=300,女生人数为500-300=200;
(2)8分对应百分数用8分的总人数÷500,10分对应百分数用1-其它几个百分数;
(3)8分以下总人数=500×10%=50,其中女生=50-20,10分总人数=500×62%=310,其中女生人数=310-180=130.
(1)如图,男生人数为20+40+60+180=300,女生人数为500-300=200,
故答案为:300,200;
(2)8分对应百分数为(40+20)÷500=12%,
10分对应百分数为1-10%-12%-16%=62%,
故答案为:a=12,b=62;
(3)解:由图得
8分以下的人数有:500×10%=50人,
∴女生有:50﹣20=30人.
得10分的女生有:62%×500﹣180=130人.
补全图象为:


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:
【题目】某校为了解学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机选取该校部分学生进行调查,要求每名学生从中只选一类最喜爱的电视节目,以下是根据调查结果绘制的不完整统计表,根据表中信息,回答下列问题:
喜爱的电视节目类型 | 人数 | 频率 |
新闻 | 4 | 0.08 |
体育 | / | / |
动画 | 15 | / |
娱乐 | 18 | 0.36 |
戏曲 | / | 0.06 |
(1)本次共调查了_______名学生,若将各类电视节目喜爱的人数所占比例绘制成扇形统计图,则“喜爱动画”对应扇形的圆心角度数是_______;
(2)该校共有2000名学生,根据调查结果估计该校“喜爱体育”节目的学生人数;
(3)在此次问卷调查中,甲、乙两班分别有![]() 人喜爱新闻节目,若从这
人喜爱新闻节目,若从这![]() 人中随机抽取
人中随机抽取![]() 人去参加“新闻小记者”培训,求抽取的
人去参加“新闻小记者”培训,求抽取的![]() 人来自不同班级的概率.
人来自不同班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(建立概念)如下图,A、B为数轴上不重合的两定点,点P也在该数轴上,我们比较线段![]() 和
和![]() 的长度,将较短线段的长度定义为点P到线段
的长度,将较短线段的长度定义为点P到线段![]() 的“靠近距离”.特别地,若线段
的“靠近距离”.特别地,若线段![]() 和
和![]() 的长度相等,则将线段
的长度相等,则将线段![]() 或
或![]() 的长度定义为点P到线段
的长度定义为点P到线段![]() 的“靠近距离”.
的“靠近距离”.
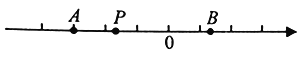
(概念理解)如下图,数轴的原点为O,点A表示的数为![]() ,点B表示的数为4.
,点B表示的数为4.
(1)点O到线段![]() 的“靠近距离”为________;
的“靠近距离”为________;
(2)点P表示的数为m,若点P到线段![]() 的“靠近距离”为3,则m的值为_________;
的“靠近距离”为3,则m的值为_________;

(拓展应用)(3)如下图,在数轴上,点P表示的数为![]() ,点A表示的数为
,点A表示的数为![]() ,点B表示的数为6. 点P以每秒2个单位长度的速度向正半轴方向移动时,点B同时以每秒1个单位长度的速度向负半轴方向移动.设移动的时间为
,点B表示的数为6. 点P以每秒2个单位长度的速度向正半轴方向移动时,点B同时以每秒1个单位长度的速度向负半轴方向移动.设移动的时间为![]() 秒,当点P到线段
秒,当点P到线段![]() 的“靠近距离”为3时,求t的值.
的“靠近距离”为3时,求t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织360名师生外出活动,计划租用甲、乙两种型号的客车;经了解,甲车每辆最多能载40人和16件行李,乙车每辆最多能载30人和20件行李.
(1)已知师生行李打包后共有164件,若租用10辆甲、乙两种型号的客车,请你帮助设计出该校所有可行的租车方案;
(2)若师生行李打包后共有m件,且170 < m ≤ 184,如果所租车辆刚好把所有师生和行李载走(每辆车均以最多承载量载满),求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】梯形ABCD中AB∥CD,∠ADC+∠BCD=90°,以AD、AB、BC为斜边向形外作等腰直角三角形,其面积分别是![]() ,且
,且![]() ,则CD=( )
,则CD=( )

A.2.5ABB.3ABC.3.5ABD.4AB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若![]() 的度数是
的度数是![]() 的度数的k倍,则规定
的度数的k倍,则规定![]() 是
是![]() 的k倍角.
的k倍角.
(1)若∠M=21°17',则∠M的5倍角的度数为 ;
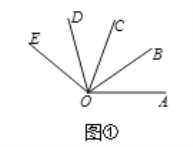
(2)如图1,OB是∠AOC的平分线,OD是∠COE的平分线,若∠AOC=∠COE,请直接写出图中∠AOB的所有3倍角;
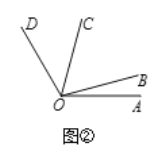
(3)如图2,若∠AOC是∠AOB的5倍角,∠COD是∠AOB的3倍角,且∠AOC和∠BOD互为补角,求∠AOD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面内,将一副直角三角板按如图所示的方式摆放,其中三角形ABC为含60°角的直角三角板,三角形BDE为含45°角的直角三角板.

(1)如图1,若点D在AB上,则∠EBC的度数为 ;
(2)如图2,若∠EBC=170°,则∠α的度数为 ;
(3)如图3,若∠EBC=118°,求∠α的度数;
(4)如图3,若0°<∠α<60°,求∠ABE-∠DBC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
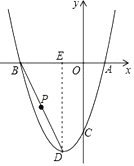
【题目】如图,已知抛物线y = x2 + bx + c的图象经过点A(l ,0) ,B(﹣3 ,0) ,与y轴交于点C ,抛物线的顶点为D ,对称轴与x轴相交于点E ,连接BD .
(1)求抛物线的解析式 .
(2)若点P在直线BD上,当PE = PC时,求点P的坐标 .
(3)在(2)的条件下,作PF⊥x轴于F ,点M为x轴上一动点 ,N为直线PF上一动点 ,G为抛物线上一动点,当以点F ,N ,G ,M 四点为顶点的四边形为正方形时,求点M的坐标 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,AD的中点,
且∠ABM=∠BAM,连接BM,MN,BN.
(1)求证:BM=MN;
(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com