
分析 多项式比较大小,采用“作差法”,将多项式因式分解,再根据已知条件判断M-N的符号.
解答 解:∵M-N=(a2b+b2c+c2a)-(ab2+bc2+ca2),
=a2b+b2c+c2a-ab2-bc2-ca2,
=a2(b-c)+b2(c-a)+c2(a-b),
=a2(b-c)+bc(b-c)-ab2+ac2,
=a2(b-c)+bc(b-c)-a(b+c)(b-c),
=(b-c)(a2+bc-ab-ac),
=(b-c)(a-c)(a-b),
又a>b>c,
∴M-N=(b-c)(a-c)(a-b)>0,
即M>N.
点评 本题考查了因式分解的实际运用,用作差法比较整式的大小是常用的方法:当M-N>0时,M>N,当M-N=0时,M=N,当M-N<0时,M<N.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
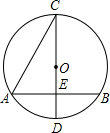 如图,AB,CD分别是⊙O的弦和直径,AB⊥CD于点E,若CD=10,AB=8,则sin∠ACD的值为( )
如图,AB,CD分别是⊙O的弦和直径,AB⊥CD于点E,若CD=10,AB=8,则sin∠ACD的值为( )| A. | 30° | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
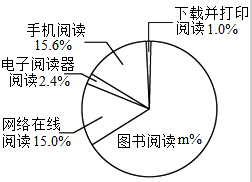 根据某研究院公布的2010-2014年我国成年国民阅读调查报告的部分相关数据,绘制的统计图表如下:
根据某研究院公布的2010-2014年我国成年国民阅读调查报告的部分相关数据,绘制的统计图表如下:| 年份 | 年人均阅读图书数量(本) |
| 2010 | 3.8 |
| 2011 | 4.1 |
| 2012 | 4.3 |
| 2013 | 4.6 |
| 2014 | 4.8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com