
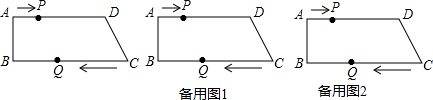
分析 (1)存在,根据对边平行且相等的四边形是平行四边形列出方程,解方程即可;
(2)存在,当APQB为矩形时,四边形PDQC为直角梯形,即AP=BQ;
(3)四边形PQCD不可能是菱形,根据邻边相等的平行四边形是菱形进行计算,比较邻边的长度得到答案.
解答 解:(1)存在;
如图1,当PD=CQ时,四边形PQCD为平行四边形,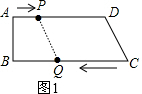
即20-2t=3t,
解得,t=4,
故当t=4时,四边形PQCD为平行四边形;
(2)存在;
如图2,当AP=BQ时,四边形PQCD为直角梯形,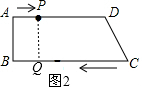
即2t=26-3t
解得:t=5.2,
故当t=5.2时,四边形PQCD为直角梯形;
(3)四边形PQCD不可能是菱形,
如图3,作DE⊥BC于E,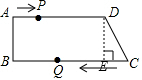
则四边形ABED为矩形,
∴DE=AB=8,EC=2,
∴CD=$\sqrt{D{E}^{2}+C{E}^{2}}$=2$\sqrt{17}$,
若四边形PQCD是菱形,则四边形PQCD是平行四边形,
根据(1)得:t=4s,
∴PD=20-8=12(cm),
∴PD≠CD,
∴四边形PQCD不可能是菱形.
点评 本题考查的是直角梯形和矩形的性质以及平行四边形、菱形的判定,掌握对边平行且相等的四边形是平行四边形、邻边相等的平行四边形是菱形是就的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
 如图,已知在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F,若∠EAF=60°,CE=3cm,FC=1cm,求AB,BC的长及ABCD面积.
如图,已知在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F,若∠EAF=60°,CE=3cm,FC=1cm,求AB,BC的长及ABCD面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
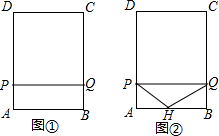 如图①,在矩形ABCD中,AB=9.AD=12.点P从点A出发以每秒3个单位长度的速度沿A-D-C-B-A运动一周到点A停止.当点P不与矩形ABCD的顶点重合时,过点P作直线PQ⊥AP,与矩形的边的另一交点为Q.设点P的运动时间为t(秒).
如图①,在矩形ABCD中,AB=9.AD=12.点P从点A出发以每秒3个单位长度的速度沿A-D-C-B-A运动一周到点A停止.当点P不与矩形ABCD的顶点重合时,过点P作直线PQ⊥AP,与矩形的边的另一交点为Q.设点P的运动时间为t(秒).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
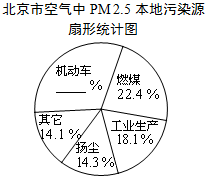 据报道,历经一年半的调查研究,北京PM 2.5源解析已经通过专家论证.各种调查显示,机动车成为PM 2.5的最大来源,一辆车一天行驶20千米,那么这辆车每天至少就要向大气里排放0.035千克污染物.如图是相关的统计图表:
据报道,历经一年半的调查研究,北京PM 2.5源解析已经通过专家论证.各种调查显示,机动车成为PM 2.5的最大来源,一辆车一天行驶20千米,那么这辆车每天至少就要向大气里排放0.035千克污染物.如图是相关的统计图表:| 空气质量等级 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
| 天数(天) | 41 | 135 | 84 | 47 | 45 | 13 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com