
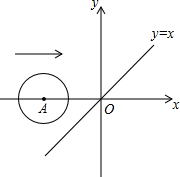
 如图,在平面直角坐标系中,x轴上一点A从点(-3.1,0)出发沿x轴向右平移,当以A为圆心,半径为2的圆与函数y=x的图象相切时,点A的坐标是
如图,在平面直角坐标系中,x轴上一点A从点(-3.1,0)出发沿x轴向右平移,当以A为圆心,半径为2的圆与函数y=x的图象相切时,点A的坐标是| 2 |
| 2 |
| 2 |
| 2 |
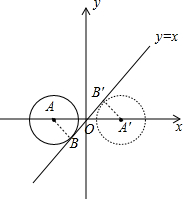 当⊙A在y轴左侧与直线y=x相切时,如图,
当⊙A在y轴左侧与直线y=x相切时,如图,| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
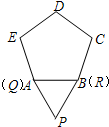 如图,将边长为1的等边△PQR沿着边长为1的正五边形ABCDE外部的边连续滚动(点Q、点R分别与点A、点B重合),当△PQR第一次回到原来的起始位置时(顶点位置与原来相同),点P所经过的路线长为( )
如图,将边长为1的等边△PQR沿着边长为1的正五边形ABCDE外部的边连续滚动(点Q、点R分别与点A、点B重合),当△PQR第一次回到原来的起始位置时(顶点位置与原来相同),点P所经过的路线长为( )A、
| ||
B、
| ||
| C、8π | ||
| D、16π |
查看答案和解析>>
科目:初中数学 来源: 题型:
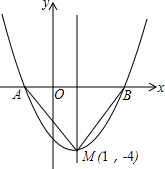 如图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,-4)
如图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,-4)| 5 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,抛物线y=x2-4x+3与x轴交于A、B两点,与y轴正半轴交于点C.在此抛物线上是否存在一点P,使直线OP与抛物线只有点P这个公共点?若存在请求出点P的坐标;若不存在,请说明理由.
如图,抛物线y=x2-4x+3与x轴交于A、B两点,与y轴正半轴交于点C.在此抛物线上是否存在一点P,使直线OP与抛物线只有点P这个公共点?若存在请求出点P的坐标;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
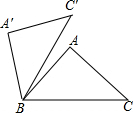 如图,在△ABC中,∠A=90°,AB=AC=3,现将△ABC绕点B逆时针旋转一定角度,点C′恰落在边BC上的高所在的直线上,则边BC在旋转过程中所扫过的面积为( )
如图,在△ABC中,∠A=90°,AB=AC=3,现将△ABC绕点B逆时针旋转一定角度,点C′恰落在边BC上的高所在的直线上,则边BC在旋转过程中所扫过的面积为( )| A、π | B、2π | C、3π | D、4π |
查看答案和解析>>
科目:初中数学 来源: 题型:
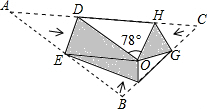 如图,将△ABC沿DE、HG、EF翻折,三个顶点均落在点O处,且EA与EB重合于线段EO,若∠DOH=78°,则∠FOG的度数为( )
如图,将△ABC沿DE、HG、EF翻折,三个顶点均落在点O处,且EA与EB重合于线段EO,若∠DOH=78°,则∠FOG的度数为( )| A、78° | B、102° |
| C、120° | D、112° |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
| A、y1<y2<y3 |
| B、y2<y1<y3 |
| C、y3<y1<y2 |
| D、y2<y3<y1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com