Question

如图1是小明在健身器材上进行仰卧起坐锻炼时情景，如图2是小明锻炼时上半身由EM位置运动到地面垂直的EN位置时的示意图，已知：BC⊥CD，AD⊥CD，BC=0.64m，AD=0.24m，AB=1.29m．

（1）求AB的倾斜角α的度数（精确到1°，友情提示：sin17°=0.2923，sin18°=0.3090，sin19°=0.3256）；

（2）若测得EN=0.88m，试计算小明头顶由M运动到N点的路径的长度．（精确到0.01m）

　

Answer 1

【考点】解直角三角形的应用-坡度坡角问题；弧长的计算．

【分析】（1）过A作AF∥DC，分别交BC，NE延长线于F，H，则四边形AFCD为矩形，AF=CD，AD=CF，可求得BF，在直角三角形ABF中，已知两边，满足解直角三角形的条件，就可求得α的值；

（2）由在直角三角形中两个锐角互余，求得∠NEM的度数，由弧长公式求得弧MN的长．

【解答】解：（1）过A作AF∥DC，分别交BC，NE延长线于F，H

∵AD⊥CD，BC⊥CD

∴AD∥BC

∴四边形AFCD为矩形

∴BF=BC﹣AD=0.4．

在Rt△ABF中，

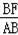
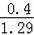
∵sinα==≈0.310，

∴α≈18°．

即AB的倾斜角度数约为18°；

 

（2）∵NE⊥AF，

∴∠AEH=90°﹣18°=72°．

∴∠MEN=180°﹣∠AEH=108°．

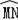
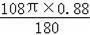
∴的长=≈1.66（米）．

答：小明头顶运动的路径的长约为1.60米．

【点评】此题主要考查了解直角三角形的应用，熟练应用锐角三角函数的概念和弧长公式是解题关键．