
����Ŀ����ͼ1��P��ӵ�A��ʼ��2����/����ٶ���A��B��C�ķ����ƶ�����Q�ӵ�C��ʼ��1����/����ٶ���C��A��B�ķ����ƶ�����ֱ��������ABC�У���A��90������AB��16���ף�AC��12���ף�BC��20���ף����P��Qͬʱ��������t���룩��ʾ�ƶ�ʱ�䣬��ô��
��1����ͼ1����P���߶�AB���˶���Q���߶�CA���˶��������tΪ��ֵʱ��QA��AP
��2����ͼ2����Q��CA���˶��������tΪ��ֵʱ��������QAB���������������ABC�����![]() ��
��
��3����ͼ3����P�㵽��C��ʱ��P��Q���㶼ֹͣ�˶�������tΪ��ֵʱ���߶�AQ�ij��ȵ����߶�BP�ij���![]()

���𰸡�(1) 4s;(2) 9s;(3) t=![]() s��16s
s��16s
��������
���⣨1����P���߶�AB���˶���Q���߶�CA���˶�ʱ����CQ=t��AP=2t����AQ=12-t����AQ=AP���ɵ÷���12-t=2t���ⷽ�̼��ɣ�
��2����Q���߶�CA��ʱ����CQ=t����AQ=12-t������������QAB���������������ABC�����![]() ���г����̼��ɽ�����⣮
���г����̼��ɽ�����⣮
��3���������������ۼ��ɢٵ�0��t��8ʱ��P���߶�AB���˶���Q���߶�CA���˶����ڵ�8��t��12ʱ��Q���߶�CA���˶���P���߶�BC���˶����۵�t��12ʱ��Q���߶�AB���˶���P���߶�BC���˶�ʱ���ֱ��г�������⼴�ɣ�
�����������1����P���߶�AB���˶���Q���߶�CA���˶�ʱ����CQ=t��AP=2t����AQ=12-t��
��AQ=AP��
��12-t=2t��
��t=4��
��t=4sʱ��AQ=AP��
��2����Q���߶�CA��ʱ����CQ=t����AQ=12-t��
��������QAB���������������ABC�����![]() ��
��
��![]() ABAQ=
ABAQ=![]() ��
��![]() ABAC��
ABAC��
��![]() ��16����12-t��=
��16����12-t��=![]() ��16��12�����t=9��
��16��12�����t=9��
��t=9sʱ��������QAB���������������ABC�����![]() ��
��
��3���������֪��Q���߶�CA���˶���ʱ��Ϊ12�룬P���߶�AB���˶�ʱ��Ϊ8�룬
�ٵ�0��t��8ʱ��P���߶�AB���˶���Q���߶�CA���˶�����CQ=t��AP=2t����AQ=12-t��BP=16-2t��
��AQ=![]() BP��
BP��
��12-t=![]() ��16-2t�������t=16������������������
��16-2t�������t=16������������������
�ڵ�8��t��12ʱ��Q���߶�CA���˶���P���߶�BC���˶�����CQ=t����AQ=12-t��BP=2t-16��
��AQ=![]() BP��
BP��
��12-t=![]() ��2t-16�������t=
��2t-16�������t=![]() ��
��
�۵�t��12ʱ��Q���߶�AB���˶���P���߶�BC���˶�ʱ��
��AQ=t-12��BP=2t-16��
��AQ=![]() BP��
BP��
��t-12=![]() ��2t-16�������/span>t=16��
��2t-16�������/span>t=16��
����������t=![]() s��16sʱ��AQ=
s��16sʱ��AQ=![]() BP��
BP��


 �·Ƿ��̸����100��ϵ�д�
�·Ƿ��̸����100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
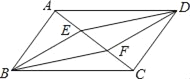
����Ŀ����ͼ������ABCD�У�E��F�ǶԽ���AC�ϵ�������AE=CF������BE=DF����BE��DF����AB=DE�����ı���EBFDΪƽ���ı��Σ���S��ADE=S��ABE����AF=CE��Щ��������ȷ����_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У����κ���y=x2+bx+c�ĶԳ���Ϊ�����㣨1��0����ֱ�ߣ���ͼ����x�ύ�ڵ�A��B���ҹ���C��0����3�����䶥��ΪD��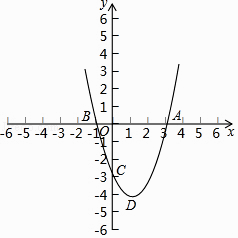
��1����������κ����Ľ���ʽ���������ꣻ
��2����y������һ��P����P���C���غϣ���ʹ�á�APD=90�㣬���P�����ꣻ
��3���ڣ�2���������£�����APD��ֱ��AD���۵õ���AQD�����Q�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ش��������⣺
��1����ͼ��ʾ�ļס�������ƽ��ͼ������ʲô�����壿

��2���ɶ��ƽ��Χ�ɵļ�������������壮��һ�������������Ϊf���������Ϊv������Ϊe���ֱ����ڣ�1�����������������f+v��e��ֵ���㷢��ʲô���ɣ�
��3��Ӧ���������ɽ�����⣺һ��������Ķ�������������8������50���⣬������������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
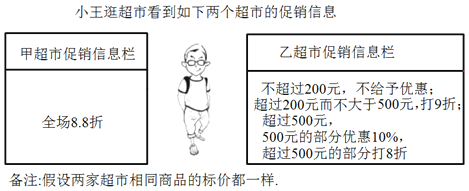
����Ŀ����1����һ���Թ������ܶ���300Ԫʱ���ס��ҳ���ʵ����ֱ��Ƕ��٣�
��2��������ܶ��Ƕ���ʱ���ס��ҳ���ʵ����һ����
��3��С�����ε��ҳ��зֱ��︶��198Ԫ��466Ԫ������ֻȥһ�θó��й���ͬ�������Ʒ�����Խ�ʡ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC�У�AB=15��BC=14��AC=13������ABC�������
ijѧϰС�龭����������������������Ľ���˼·�����㰴�����ǵĽ���˼·��ɽ����̣�
˼·����1�� ��AD��BC��D����BD = x���ú�x�Ĵ���ʽ��ʾCD����2�����ݹ��ɶ���������AD��Ϊ������������������ģ�������x����3�����ù��ɶ������AD�ij����ټ������������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
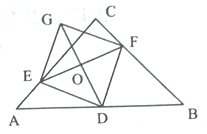
����Ŀ����ͼ���ڵ���ֱ��������ABC�У���ACB=90![]() ��AC=BC=4��DΪAB���е㣬E��F�ֱ���AC�� BC�ϵĵ㣨��E����˵�A��C�غϣ�����AE=CF������EF��ȡEF���е�O������DO���ӳ�����G��ʹGO=OD������DE�� GE�� GF��
��AC=BC=4��DΪAB���е㣬E��F�ֱ���AC�� BC�ϵĵ㣨��E����˵�A��C�غϣ�����AE=CF������EF��ȡEF���е�O������DO���ӳ�����G��ʹGO=OD������DE�� GE�� GF��
(1)��֤���ı���EDFG�������Σ�
(2)ֱ��д���ı���EDFG�������Сֵ��E�����ڵ�λ�ã�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ�˽ⱾУ���꼶�������������ϡ���Ŀ��ѵ������������ȡ���꼶��������������һ�β��ԣ�����15�֣��ɼ�����Ϊ�����֣����������Գɼ�����λ���֣��ֳ����ࣺA�ࣨ12��m��15����B�ࣨ9��m��11����C�ࣨ6��m��8����D�ࣨm��5�����Ƴ�����������������ͳ��ͼ�������ͼ����Ϣ����������⣺ 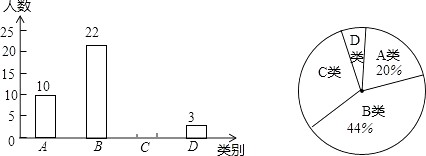
��1�����γ�ȡ��������Ϊ �� ����ͳ��ͼ��A�����Ե�Բ�Ľ����ȣ�
��2���벹ȫ����ͳ��ͼ��
��3������У���꼶������600��������Ƹ�У���꼶�������������ϡ���Ŀ�ɼ�ΪC����ж�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������
��1��20170��|��sin45��|cos45��+ ![]() ������
������ ![]() ����1
����1
��2�� ��
��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com