
����Ŀ����֪����y����![]() ��x��0����y��
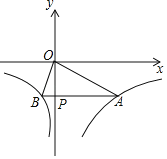
��x��0����y��![]() ��x��0����ͼ����ͼ��ʾ����P��y�Ḻ������һ���㣬����P��y��Ĵ��߽�ͼ����A��B���㣬����OA��OB�����н��ۣ�������M1��x1��y1����M2��x2��y2����ͼ���ϣ���x1��x2��0����y1��y2���ڵ���P����Ϊ��0����3��ʱ����AOB�ǵ��������Σ������۵�P��ʲôλ�ã�ʼ����S��AOB��7.5��AP��4BP���ܵ���P�ƶ���ʹ��AOB��90��ʱ����A������Ϊ��2
��x��0����ͼ����ͼ��ʾ����P��y�Ḻ������һ���㣬����P��y��Ĵ��߽�ͼ����A��B���㣬����OA��OB�����н��ۣ�������M1��x1��y1����M2��x2��y2����ͼ���ϣ���x1��x2��0����y1��y2���ڵ���P����Ϊ��0����3��ʱ����AOB�ǵ��������Σ������۵�P��ʲôλ�ã�ʼ����S��AOB��7.5��AP��4BP���ܵ���P�ƶ���ʹ��AOB��90��ʱ����A������Ϊ��2![]() ����
����![]() ����������ȷ�Ľ���Ϊ___��
����������ȷ�Ľ���Ϊ___��
���𰸡��ڢۢܣ�
��������
�ٴ�����x1��x2��0ʱ������y��x���������С�ɵã�
����ȷ�����A��B�������꼴�ɽ�����⣻
����ȷ����P��0��m������B��![]() ��m����A����
��m����A����![]() ��m�������PA��PB���Ƴ�PA��4PB����SAOB��S��OPB+S��OPA�������S��AOB��7.5��
��m�������PA��PB���Ƴ�PA��4PB����SAOB��S��OPB+S��OPA�������S��AOB��7.5��
����ȷ����P��0��m������B��![]() ��m����A����
��m����A����![]() ��m�����Ƴ�PB����
��m�����Ƴ�PB����![]() ��PA����
��PA����![]() ��OP����m���ɡ�OPB�ס�APO���ɵ�OP2��PBPA���г����̼��ɽ�����⣮
��OP����m���ɡ�OPB�ס�APO���ɵ�OP2��PBPA���г����̼��ɽ�����⣮
�⣺�ٴ���x1��x2��0������y��x���������С��
��y1��y2���ʢٴ���
����ȷ����P��0����3����
��B����1����3����A��4����3����
��AB��5��OA��![]() ��5��
��5��
��AB��AO��
���AOB�ǵ��������Σ��ʢ���ȷ��
����ȷ����P��0��m������B��![]() ��m����A����
��m����A����![]() ��m����
��m����
��PB����![]() ��PA����
��PA����![]() ��
��
��PA��4PB��
��SAOB��S��OPB+S��OPA��![]() +
+![]() ��7.5���ʢ���ȷ��
��7.5���ʢ���ȷ��
����ȷ����P��0��m������B��![]() ��m����A����
��m����A����![]() ��m����
��m����
��PB����![]() ��PA����
��PA����![]() ��OP����m��
��OP����m��
�ߡ�
���BOP+��AOP��90������AOP+��OAP��90����
���BOP����OAP��
���OPB�ס�APO��
��![]() ��
��![]() ��
��
��OP2��PBPA��
��m2����![]() ����
����![]() ����
����
��m4��36��
��m��0��
��m����![]() ��
��
��A��2![]() ����
����![]() �����ʢ���ȷ��
�����ʢ���ȷ��
��ڢۢ���ȷ��
�ʴ�Ϊ���ڢۢܣ�




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
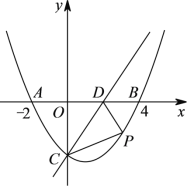
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y=ax2+bx+c��a��0����x�ύ�ڵ�A(-2��0)��B(4��0)����ֱ��![]() ���ڵ�C(0��-3)��ֱ��
���ڵ�C(0��-3)��ֱ��![]() ��x�ύ�ڵ�D��
��x�ύ�ڵ�D��
��1����������ߵĽ���ʽ��
��2����P���������ϵ��������ϵ�һ�����㣬����PC��PD������PCD��������ʱ�����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��P�Ǿ���ABCD�ڲ���һ���㣬M��AB����һ���㣬����MP���ӳ������ABCD��һ�߽��ڵ�N������AN����֪AB��6cm����A��M�����ľ���Ϊxcm��M��N�����ľ���Ϊy1cm��A��N�����ľ���Ϊy2cm��С������ѧϰ�����ľ��飬�ֱ�Ժ���y1��y2���Ա���x�ı仯���仯�Ĺ��ɽ�����̽����������С����̽�����̣��벹��������
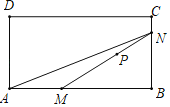
��1������������Ա���x��ֵ����ȡ�㡢��ͼ���������ֱ�õ���y1��y2��x�ļ����Ӧֵ��
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 6.30 | 5.40 | �� �� | 4.22 | 3.13 | 3.25 | 4.52 |
y2/cm | 6.30 | 6.34 | 6.43 | 6.69 | 5.75 | 4.81 | 3.98 |
��2����ͬһƽ��ֱ������ϵxOy�У�����Բ�ȫ��ı��и����Ӧֵ����Ӧ�ĵ㣨x��y1��������������y1��ͼ��
��3����Ϻ���ͼ������⣺����AMNΪ����������ʱ��AM�ij���ԼΪ�� ��cm��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
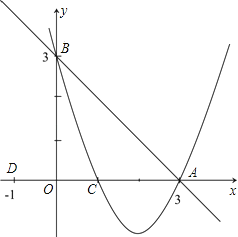
����Ŀ����ͼ����֪��ֱ��![]() ��x���ڵ�A����y���ڵ�B��������y=ax2+bx+c����A��B��C��1��0�����㣮
��x���ڵ�A����y���ڵ�B��������y=ax2+bx+c����A��B��C��1��0�����㣮
��1���������ߵĽ���ʽ��
��2������D������Ϊ��-1��0������ֱ��![]() ����һ��P,ʹ��ABO����ADP���ƣ������P�����ꣻ
����һ��P,ʹ��ABO����ADP���ƣ������P�����ꣻ
��3���ڣ�2���������£���x���·����������ϣ��Ƿ���ڵ�E��ʹ��ADE����������ı���APCE�������������ڣ��������E�����ꣻ��������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵȱ���ABC�У�D��E��F�ֱ���BC��AC��AB�ϵĵ㣬DE��AC��EF��AB��
FD��BC������DEF���������ABC�����֮�ȵ����� ��

A��1��3 B��2��3 C��![]() ��2 D��
��2 D��![]() ��3
��3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
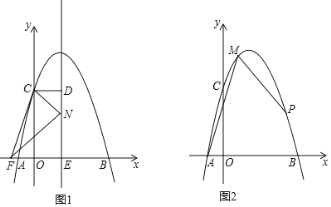
����Ŀ�����κ���y=ax2+bx+4��ͼ����x�ύ������A��B����y�ύ�ڵ�C����A(1��0)��B(4��0)��
(1)��˶��κ����ı���ʽ��
(2)��ͼ1�������ߵĶԳ���m��x�ύ�ڵ�E��CD��m������ΪD����F(![]() ��0)������N���߶�DE���˶�������CF��CN��FN�����Ե�C��D��NΪ���������������FEN���ƣ����N�����ꣻ
��0)������N���߶�DE���˶�������CF��CN��FN�����Ե�C��D��NΪ���������������FEN���ƣ����N�����ꣻ
(3)��ͼ2����M���������ϣ��ҵ�M�ĺ�������1����PΪ��������һ���㣬����PMA=45�������P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧΪ�˽�ѧ�������š����������֡�����������ӽ�Ŀ��ϲ�������������ͳ�Ƶ���![]() ���������ij������ͬѧ��ϲ���Ľ�Ŀ
���������ij������ͬѧ��ϲ���Ľ�Ŀ![]() ÿ��ѧ����ѡ��ֻ��ѡ�������Ŀ�е�һ��
ÿ��ѧ����ѡ��ֻ��ѡ�������Ŀ�е�һ��![]() ����������������²�������ͳ��ͼ
����������������²�������ͳ��ͼ![]() ������ͼ�ṩ����Ϣ���ش��������⣺
������ͼ�ṩ����Ϣ���ش��������⣺
![]() ��ϲ���������Ŀ����______�ˣ�ͼ��
��ϲ���������Ŀ����______�ˣ�ͼ��![]() ______��
______��
![]() �벹ȫ����ͳ��ͼ��
�벹ȫ����ͳ��ͼ��
![]() ���ݳ���������������У��1800��ѧ����������Ƹ�У�ж�����ѧ����ϲ���������Ŀ��
���ݳ���������������У��1800��ѧ����������Ƹ�У�ж�����ѧ����ϲ���������Ŀ��
![]() ��ȫ��ͬѧ�У��мס��ҡ���������ͬѧ��ϲ���������Ŀ�������δ���Ӽס��ҡ�������4��ͬѧ��ѡȡ2�˲μ�ѧУ��֯������֪ʶ�����������б�������״ͼ��ͬʱѡ�мס�����ͬѧ�ĸ��ʣ�
��ȫ��ͬѧ�У��мס��ҡ���������ͬѧ��ϲ���������Ŀ�������δ���Ӽס��ҡ�������4��ͬѧ��ѡȡ2�˲μ�ѧУ��֯������֪ʶ�����������б�������״ͼ��ͬʱѡ�мס�����ͬѧ�ĸ��ʣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
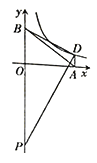
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A��B�ֱ���x�ᡢy����������ϣ�OA=4��AB=5����D�ڷ���������![]() ��k>0����ͼ���ϣ�
��k>0����ͼ���ϣ�![]() ����P��y�Ḻ�����ϣ�OP=7.
����P��y�Ḻ�����ϣ�OP=7.
��1�����B��������߶�PB�ij���
��2����![]() ʱ�����������Ľ���ʽ��
ʱ�����������Ľ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ijУ��֯��һ�Ρ�ʫ�ʴ�ᡱ������ʦΪ��ѡ�α���ѧ���μӣ��Ա���ȫ��ѧ��ʫ�ʵ�������������˵��飬������������Ϊ�����ࣺA���ã�B���У�C��������ͼ����Ϣ������������⣺
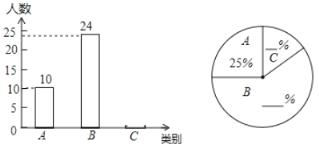
��1��ȫ��ѧ�������� ���ˣ�
��2������ͳ��ͼ�У�B��ռ�İٷֱ�Ϊ�� ��%��C��ռ�İٷֱ�Ϊ�� ��%��
��3�������������ͳ��ͼ����������
��4��С����ѡ�вμ��˱�������������һ���ش����ǣ����±���ʾ�ľŹ�����ѡȡ�߸������һ��ʫ�����Ϊ������ʫ�鵽��������С���ش������ʱ���Ե��ĸ�����ѡ���顱����ѡ���ࡱ�����߸�����ѡ����������ѡ�������������Ծ������ֱ����ѡ�������б�����״ͼ�ķ�����С���ش���ȷ�ĸ��ʣ�
�� | �� | �� |
�� | ʫ | �� |
�� | �� | �� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com