
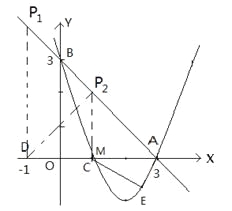
【题目】如图,已知:直线![]() 交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A、B、C(1,0)三点.
交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A、B、C(1,0)三点.
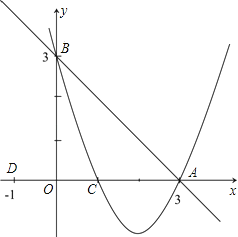
(1)求抛物线的解析式;
(2)若点D的坐标为(-1,0),在直线![]() 上有一点P,使ΔABO与ΔADP相似,求出点P的坐标;
上有一点P,使ΔABO与ΔADP相似,求出点P的坐标;
(3)在(2)的条件下,在x轴下方的抛物线上,是否存在点E,使ΔADE的面积等于四边形APCE的面积?如果存在,请求出点E的坐标;如果不存在,请说明理由.
【答案】(1)![]() ;(2)(1,2),
;(2)(1,2),![]() ;(3)不存在,理由见解析.
;(3)不存在,理由见解析.
【解析】
解:(1):由题意得,A(3,0),B(0,3)
∵抛物线经过A、B、C三点,∴把A(3,0),B(0,3),C(1,0)三点分别代入![]() 得方程组
得方程组
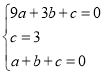
解得: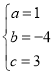
∴抛物线的解析式为![]()
(2)由题意可得:△ABO为等腰三角形,如图所示,
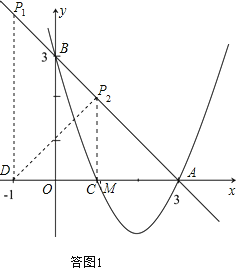
若△ABO∽△AP1D,则![]()
∴DP1=AD=4
∴P1![]()
若△ABO∽△ADP2 ,过点P2作P2 M⊥x轴于M,AD=4
∵△ABO为等腰三角形, ∴△ADP2是等腰三角形,由三线合一可得:DM=AM=2= P2M,即点M与点C重合
∴P2(1,2)
(3)如图设点E![]() ,则
,则
![]()
①当P1(-1,4)时,
S四边形AP1CE=S三角形ACP1+S三角形ACE
![]()
=![]()
∴![]() ∴
∴![]()
∵点E在x轴下方 ∴![]()
代入得:![]() ,即
,即![]()
∵△=(-4)2-4×7=-12<0
∴此方程无解
②当P2(1,2)时,S四边形AP2CE=S三角形ACP2+S三角形ACE=![]()
∴![]() ∴
∴![]()
∵点E在x轴下方 ∴![]() 代入得:
代入得:![]()
即![]() ,∵△=(-4)2-4×5=-4<0
,∵△=(-4)2-4×5=-4<0
∴此方程无解
综上所述,在x轴下方的抛物线上不存在这样的点E.


 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:
【题目】在长方形ABCD中,AB=3,BC=4,动点P从点A开始按A→B→C→D的方向运动到点D.如图,设动点P所经过的路程为x,△APD的面积为y.(当点P与点A或D重合时,y=0)
(1)写出y与x之间的函数解析式;
(2)画出此函数的图象.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:有一组邻边相等且有一组对角互补的凸四边形叫做等补四边形
(1)概念理解
①根据上述定义举一个等补四边形的例子:
②如图1,四边形ABCD中,对角线BD平分∠ABC,∠A+∠C=180°,求证:四边形ABCD是等补四边形
(2)性质探究:
③小明在探究时发现,由于等补四边形有一组对角互补,可得等补四边形的四个顶点共圆,如图2,等补四边形ABCD内接于⊙O,AB=AD,则∠ACD ∠ACB(填“>”“<”或“=“);
④若将两条相等的邻边叫做等补四边形的“等边”,等边所夹的角叫做“等边角”,它所对的角叫做“等边补角”连接它们顶点的对角线叫做“等补对角线”,请用语言表述③中结论:
(3)问题解决
在等补四边形ABCD中,AB=BC=2,等边角∠ABC=120°,等补对角线BD与等边垂直,求CD的长.
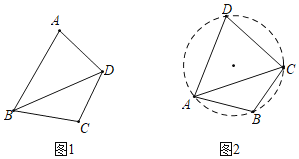
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数L与y轴交于点C(0,3),且过点(1,0),(3,0).
(1)求二次函数L的解析式及顶点H的坐标
(2)已知x轴上的某点M(t,0);若抛物线L关于点M对称的新抛物线为L′,且点C、H的对应点分别为C′,H′;试说明四边形CHC′H′为平行四边形.
(3)若平行四边形的边与某一条对角线互相垂直时,称这种平行四边形为“和谐四边形”;在(2)的条件下,当平行四边形CHC′H′为“和谐四边形”时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,E为边BC上的点,且AB=AE,D为线段BE的中点,过点E作EF⊥AE,过点A作AF∥BC,且AF、EF相交于点F.

(1)求证:∠C=∠BAD;
(2)求证:AC=EF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与x轴交于
与x轴交于![]() 、B两点,与y轴交点C的坐标为
、B两点,与y轴交点C的坐标为![]() ,
,![]() 为抛物线顶点,连结AD,点M为线段AD上动点(不含端点),BM与y轴交于点N.
为抛物线顶点,连结AD,点M为线段AD上动点(不含端点),BM与y轴交于点N.
(1)求抛物线解析式;
(2)是否存在点M使得![]() 与
与![]() 相似,若存在请求出点M的坐标,若不存在,请说明理由;
相似,若存在请求出点M的坐标,若不存在,请说明理由;
(3)求当BM将四边形ABCM分为面积相等的两部分时ON的长度.
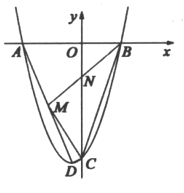
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与x轴交于点
与x轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过
经过![]() 两点且与x轴的负半轴交于点
两点且与x轴的负半轴交于点![]() .
.
![]() 求该抛物线的解析式;
求该抛物线的解析式;
![]() 若点
若点![]() 为直线
为直线![]() 上方抛物线上的一个动点,当
上方抛物线上的一个动点,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
![]() 已知
已知![]() 分别是直线
分别是直线![]() 和抛物线上的动点,当
和抛物线上的动点,当![]() 为顶点的四边形是平行四边形时,直接写出所有符合条件的
为顶点的四边形是平行四边形时,直接写出所有符合条件的![]() 点的坐标.
点的坐标.
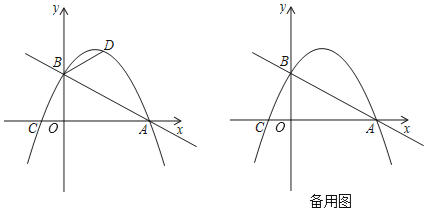
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司生产的一种产品按照质量由高到低分为A,B,C,D四级,为了增加产量、提高质量,该公司改进了一次生产工艺,使得生产总量增加了一倍.为了解新生产工艺的效果,对改进生产工艺前、后的四级产品的占比情况进行了统计,绘制了如下扇形图:
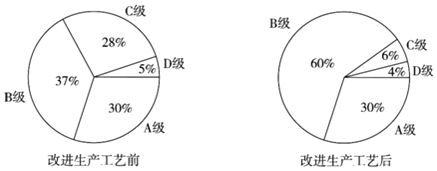
根据以上信息,下列推断合理的是( )
A.改进生产工艺后,A级产品的数量没有变化
B.改进生产工艺后,B级产品的数量增加了不到一倍
C.改进生产工艺后,C级产品的数量减少
D.改进生产工艺后,D级产品的数量减少
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com