
【题目】如图,在△ABC中,∠BAC=90°,E为边BC上的点,且AB=AE,D为线段BE的中点,过点E作EF⊥AE,过点A作AF∥BC,且AF、EF相交于点F.

(1)求证:∠C=∠BAD;
(2)求证:AC=EF.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】定义:如果一个数的平方等于﹣1,记为i2=﹣1,这个数i叫做虚数单位,把形如a+bi(a,b为实数)的数叫做复数,其中a叫这个复数的实部,b叫做这个复数的虚部,它的加、减运算与整式的加、减运算类似.复数的乘方意义与有理数的乘方的意义类似,例如:
(1)i3=iii=i2i=﹣i
(2)(2﹣i)+(5+3i)=(2+5)+(﹣1+3)i=7+2i
根据以上信息,完成下列问题:
(1)填空:(﹣1+i)(1﹣i)= ;i﹣4= .
(2)化简:i+i2+i3+i4+…+i2017.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设立了一个可以自由转动的转盘,并规定顾客消费![]() 元以上,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红、黄或绿色区域,顾客就可以分别获得
元以上,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红、黄或绿色区域,顾客就可以分别获得![]() 元,
元,![]() 元、
元、![]() 元的购物券(转盘被等分成
元的购物券(转盘被等分成![]() 个扇形).
个扇形).
![]() 顾客张吉祥消费
顾客张吉祥消费![]() 元,他获得购物券的概率是多少?
元,他获得购物券的概率是多少?
![]() 他得到
他得到![]() 元,
元,![]() 元、
元、![]() 元购物券的概率分别是多少?
元购物券的概率分别是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 是线段
是线段![]() 上的任意一点(端点除外),分别以
上的任意一点(端点除外),分别以![]() ,
,![]() 为斜边并且在
为斜边并且在![]() 的同一侧作等腰直角
的同一侧作等腰直角![]() 和
和![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,给出以下三个结论:①
,给出以下三个结论:①![]() ;②
;②![]() ;③
;③![]() ,其中正确结论的个数是( )
,其中正确结论的个数是( )

A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C在BA的延长线上,CA=AO,点D在⊙O上,∠ABD=30°.
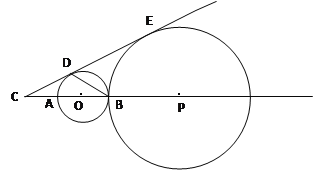
⑴求证:CD是⊙O的切线;
⑵若点P在直线AB上,⊙P与⊙O外切于点B,与直线CD相切于点E,设⊙O与⊙P的半径分别为r与R,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=16,O为AB中点,点C在线段OB上(不与点O,B重合),将OC绕点O逆时针旋转270°后得到扇形COD,AP,BQ分别切优弧![]() 于点P,Q,且点P, Q在AB异侧,连接OP.
于点P,Q,且点P, Q在AB异侧,连接OP.
(1)求证:AP=BQ;
(2)当BQ=4![]() 时,求扇形COQ的面积及
时,求扇形COQ的面积及![]() 的长(结果保留π);
的长(结果保留π);
(3)若△APO的外心在扇形COD的内部,请直接写出OC的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中(请补画出必要的图形),O为坐标原点,直线y= -2x+4与x、y轴分别交于A、B两点,过线段OA的中点C作x轴的垂线l,分别与直线AB交于点D,与直线y=x+n交于点P。
(1)直接写出点A、B、C、D的坐标:A( ),B( ),C( ),D( )
(2)若△APD的面积等于1,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】画出函数y=2x+1的图象,利用图象求:
(1)方程2x+1=0的根;
(2)不等式2x+1≥0的解集;
(3)当y≤3时,求x的取值范围;
(4)当﹣3≤y≤3时,求x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com