
【题目】如图,已知![]() 是线段
是线段![]() 上的任意一点(端点除外),分别以
上的任意一点(端点除外),分别以![]() ,
,![]() 为斜边并且在
为斜边并且在![]() 的同一侧作等腰直角
的同一侧作等腰直角![]() 和
和![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,给出以下三个结论:①
,给出以下三个结论:①![]() ;②
;②![]() ;③
;③![]() ,其中正确结论的个数是( )
,其中正确结论的个数是( )

A. 0 B. 1 C. 2 D. 3
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里,装有四个分别写有数字![]() 、
、![]() 、
、![]() 、
、![]() 的乒乓球(形状、大小一样),先从盒子里随机摸出一个乒乓球,记下数字后放回盒子,摇匀后再随机摸出一个乒乓球,记下数字.
的乒乓球(形状、大小一样),先从盒子里随机摸出一个乒乓球,记下数字后放回盒子,摇匀后再随机摸出一个乒乓球,记下数字.
![]() 请用树形图或列表法求两次摸出乒乓球上的数字相同的概率;
请用树形图或列表法求两次摸出乒乓球上的数字相同的概率;
![]() 若再向盒子里放入
若再向盒子里放入![]() 个写有数字
个写有数字![]() 的乒乓球,使得从盒子里随机摸出一个乒乓球,摸到写有数字
的乒乓球,使得从盒子里随机摸出一个乒乓球,摸到写有数字![]() 的乒乓球的概率为
的乒乓球的概率为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10.若将△PAC绕点A逆时针旋转后,得到△P′AB.
(1)求点P与点P′之间的距离;
(2)求∠APB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁四位同学进行一次乒乓球单打比赛,要从中选出两位同学打第一场比赛.
![]() 若已确定甲打第一场,再从其余三位同学中随机选取一位,求恰好选中乙同学的概率.
若已确定甲打第一场,再从其余三位同学中随机选取一位,求恰好选中乙同学的概率.
![]() 请用树状图法或列表法,求恰好选中甲、乙两位同学的概率.
请用树状图法或列表法,求恰好选中甲、乙两位同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,E为边BC上的点,且AB=AE,D为线段BE的中点,过点E作EF⊥AE,过点A作AF∥BC,且AF、EF相交于点F.

(1)求证:∠C=∠BAD;
(2)求证:AC=EF.
查看答案和解析>>
科目:初中数学 来源: 题型:
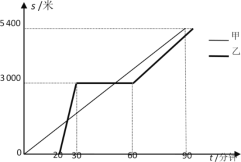
【题目】某景区在同一线路上顺次有三个景点A,B,C,甲、乙两名游客从景点A出发,甲步行到景点C;乙花20分钟时间排队后乘观光车先到景点B,在B处停留一段时间后,再步行到景点C.甲、乙两人离景点A的路程s(米)关于时间t(分钟)的函数图像如图所示.
(1)甲的速度是 米/分钟;
(2)当20≤t ≤30时,求乙离景点A的路程s与t的函数表达式;
(3)乙出发后多长时间与甲在途中相遇?
(4)若当甲到达景点C时,乙与景点C的路程为360米,则乙从景点B步行到景点C的速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC与BD交于点O.过点C作BD的平行线,过点D作AC的平行线,两直线相交于点E.
(1)求证:四边形OCED是矩形;
(2)若CE=1,DE=2,ABCD的面积是 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com