Question

【题目】画出函数y＝2x+1的图象，利用图象求：

（1）方程2x+1＝0的根；

（2）不等式2x+1≥0的解集；

（3）当y≤3时，求x的取值范围；

（4）当﹣3≤y≤3时，求x的取值范围．

Answer 1

【答案】（1）x=；（2）x≥；（3）x1；（4）2x1

【解析】

首先求出直线与坐标轴的交点坐标，经过两点画直线．然后观察图象即可求得答案．

(1)方程2x+1＝0的解是指直线与x轴的交点坐标；

(2)不等式2x+1≥0的解是指y≥0的部分；

(3) 当y≤3时, 找到对应的点，即可求得x的取值范围;

(4)当﹣3≤y≤3时，找到对应的点，即可求得x的取值范围．

解：当x=0时，y=1；当y=0时，x=，
∴直线过点 (0,1)，(,0)，
作函数y＝2x+1的图象，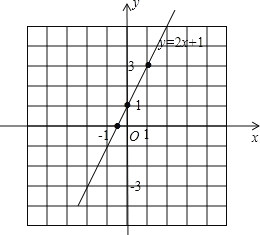

(1)由图象得，方程2x+1＝0的解为，x=；
(2)由图象得，不等式2x+1≥0的解为，x≥；

(3) 当y=3时，由3=2x+1得x=1，

∴由图象得，当y≤3时，x的取值范围为，x1，

(4)当y=3时，由3=2x+1得x=2;

当y=3时，由3=2x+1得x=1，

∴由图象得，当﹣3≤y≤3时，x的取值范围为，2x1．