
【题目】如图,AB=16,O为AB中点,点C在线段OB上(不与点O,B重合),将OC绕点O逆时针旋转270°后得到扇形COD,AP,BQ分别切优弧![]() 于点P,Q,且点P, Q在AB异侧,连接OP.
于点P,Q,且点P, Q在AB异侧,连接OP.
(1)求证:AP=BQ;
(2)当BQ=4![]() 时,求扇形COQ的面积及
时,求扇形COQ的面积及![]() 的长(结果保留π);
的长(结果保留π);
(3)若△APO的外心在扇形COD的内部,请直接写出OC的取值范围.

【答案】(1)见解析;(2)![]() ;(3)4<OC<8.
;(3)4<OC<8.
【解析】
试题(1)连接OQ.只要证明Rt△APO≌Rt△BQO即可解决问题;
(2)求出优弧DQ的圆心角以及半径即可解决问题;
(3)由△APO的外心是OA的中点,OA=8,推出△APO的外心在扇形COD的内部时,OC的取值范围为4<OC<8;
试题解析:(1)证明:连接OQ.
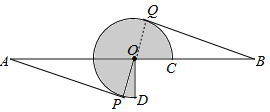
∵AP、BQ是⊙O的切线,∴OP⊥AP,OQ⊥BQ,∴∠APO=∠BQO=90°,在Rt△APO和Rt△BQO中,∵OA=OB,OP=OQ,∴Rt△APO≌Rt△BQO,∴AP=BQ;
(2)∵Rt△APO≌Rt△BQO,∴∠AOP=∠BOQ,∴P、O、Q三点共线,∵在Rt△BOQ中,cosB=![]() ,∴∠B=30°,∠BOQ=60°,∴OQ=
,∴∠B=30°,∠BOQ=60°,∴OQ=![]() OB=4,∵∠COD=90°,∴∠QOD=90°+60°=150°,∴优弧
OB=4,∵∠COD=90°,∴∠QOD=90°+60°=150°,∴优弧![]() 的长=
的长=![]() =
=![]() ;
;
(3)∵△APO的外心是OA的中点,OA=8,∴△APO的外心在扇形COD的内部时,OC的取值范围为4<OC<8.


科目:初中数学 来源: 题型:
【题目】为了响应“低碳环保,绿色出行”的公益活动,小燕和妈妈决定周日骑自行车去图书馆借书.她们同时从家出发,小燕先以150米/分的速度骑行一段时间,休息了5分钟,再以m米/分钟的速度到达图书馆,而妈妈始终以120米/分钟的速度骑行,两人行驶的路程y(米)与时间x(分钟)的关系如图,请结合图像,解答下列问题:
(1)图书馆到小燕家的距离是 米;
(2)a= ,b= ,m= ;
(3)妈妈行驶的路程y(米)关于时间x(分钟)的函数解析式是 ;定义域是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁四位同学进行一次乒乓球单打比赛,要从中选出两位同学打第一场比赛.
![]() 若已确定甲打第一场,再从其余三位同学中随机选取一位,求恰好选中乙同学的概率.
若已确定甲打第一场,再从其余三位同学中随机选取一位,求恰好选中乙同学的概率.
![]() 请用树状图法或列表法,求恰好选中甲、乙两位同学的概率.
请用树状图法或列表法,求恰好选中甲、乙两位同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,E为边BC上的点,且AB=AE,D为线段BE的中点,过点E作EF⊥AE,过点A作AF∥BC,且AF、EF相交于点F.

(1)求证:∠C=∠BAD;
(2)求证:AC=EF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区在同一线路上顺次有三个景点A,B,C,甲、乙两名游客从景点A出发,甲步行到景点C;乙花20分钟时间排队后乘观光车先到景点B,在B处停留一段时间后,再步行到景点C.甲、乙两人离景点A的路程s(米)关于时间t(分钟)的函数图像如图所示.
(1)甲的速度是 米/分钟;
(2)当20≤t ≤30时,求乙离景点A的路程s与t的函数表达式;
(3)乙出发后多长时间与甲在途中相遇?
(4)若当甲到达景点C时,乙与景点C的路程为360米,则乙从景点B步行到景点C的速度是多少?
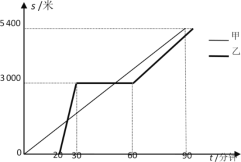
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数![]() 的图象与性质.小东根据学习函数的经验,对函数
的图象与性质.小东根据学习函数的经验,对函数![]() 的图象与性质进行了探究.下面是小东的探究过程,请补充完整:
的图象与性质进行了探究.下面是小东的探究过程,请补充完整:
(1)函数![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)下表是x与y的几组对应值.
| ... |
|
|
|
|
|
|
| 1 | 2 | 3 | ... |
| ... |
|
|
|
|
|
|
|
|
| m | ... |
求m的值;
(3)如图,在平面直角坐标系中,已描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;

(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是(1,![]() ).结合函数的图象,写出该函数的其它性质(写两条即可).
).结合函数的图象,写出该函数的其它性质(写两条即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC与BD交于点O.过点C作BD的平行线,过点D作AC的平行线,两直线相交于点E.
(1)求证:四边形OCED是矩形;
(2)若CE=1,DE=2,ABCD的面积是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=﹣x+5的图象与反比例函数y2=![]() (k≠0)在第一象限的图象交于A(1,n)和B两点.
(k≠0)在第一象限的图象交于A(1,n)和B两点.
(1)求反比例函数的解析式;
(2)当y2>y1>0时,写出自变量x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半圆O与等腰直角三角形两腰CA,CB分别切于D,E两点,直径FG在AB上,若BG=![]() -1,则△ABC的周长为( )
-1,则△ABC的周长为( )

A. 4+2![]() B. 6 C. 2+2
B. 6 C. 2+2![]() D. 4
D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com