
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§LгыyжсНЛгкЕуC(0ЃЌ3)ЃЌЧвЙ§Еу(1ЃЌ0)ЃЌ(3ЃЌ0)ЃЎ
(1)ЧѓЖўДЮКЏЪ§LЕФНтЮіЪНМАЖЅЕуHЕФзјБъ
(2)вбжЊxжсЩЯЕФФГЕуM(tЃЌ0)ЃЛШєХзЮяЯпLЙигкЕуMЖдГЦЕФаТХзЮяЯпЮЊLЁфЃЌЧвЕуCЁЂHЕФЖдгІЕуЗжБ№ЮЊCЁфЃЌHЁфЃЛЪдЫЕУїЫФБпаЮCHCЁфHЁфЮЊЦНааЫФБпаЮЃЎ
(3)ШєЦНааЫФБпаЮЕФБпгыФГвЛЬѕЖдНЧЯпЛЅЯрДЙжБЪБЃЌГЦетжжЦНааЫФБпаЮЮЊЁАКЭаГЫФБпаЮЁБЃЛдк(2)ЕФЬѕМўЯТЃЌЕБЦНааЫФБпаЮCHCЁфHЁфЮЊЁАКЭаГЫФБпаЮЁБЪБЃЌЧѓtЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉ y=x2Љ4x+3ЃЌ(2,Љ1)ЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉ t=![]() Лђ4ЛђЉ6
Лђ4ЛђЉ6
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУД§ЖЈЯЕЪ§ЗЈПЩЧѓНтЮіЪНЃЌгЩХфЗНЗЈПЩЧѓЖЅЕузјБъЃЛ
ЃЈ2ЃЉгЩжааФЖдГЦЕФаджЪПЩЕУCM=C'MЃЌHM=H'MЃЌПЩЕУНсТлЃЛ
ЃЈ3ЃЉЗжЫФжжЧщПіЬжТлЃЌгЩСНЕуОрРыЙЋЪНКЭвЛДЮКЏЪ§ЕФаджЪПЩЧѓНтЃЎ
ЃЈ1ЃЉЩшЖўДЮКЏЪ§LЕФНтЮіЪНЮЊЃКy=ax2+bx+c(aЁй0)
гЩЬтвтПЩЕУЃК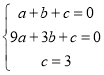
НтЕУЃК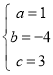
ЁрЖўДЮКЏЪ§LЕФНтЮіЪНЮЊЃКy=x2Љ4x+3ЃЌ
Ёпy=x2Љ4x+3=(xЉ2)2Љ1ЃЌ
ЁрЖЅЕуHЕФзјБъ(2,Љ1)
ЙЪД№АИЮЊЃКy=x2Љ4x+3ЃЌ(2,Љ1)
ЃЈ2ЃЉ
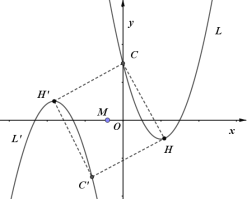
ЁпШєХзЮяЯпLЙигкЕуMЖдГЦЕФаТХзЮяЯпЮЊLЁфЃЌЧвЕуCЁЂHЕФЖдгІЕуЗжБ№ЮЊCЁфЃЌHЁфЃЛ
ЁрCM=C'MЃЌHM=H'MЃЌ
ЁрЫФБпаЮCHCЁфHЁфЮЊЦНааЫФБпаЮЃЛ
ЃЈ3ЃЉЁпЕуC(0,3)ЃЌЕуH(2,Љ1)
ЁржБЯпCHНтЮіЪНЮЊЃКy=Љ2x+3ЃЛ
ШєCC'ЁЭCHЪБЃЌдђCC'НтЮіЪНЮЊЃК![]()
ЕБy=0ЪБЃЌ![]()
Ёрt=Љ6ЃЛ
ШєHH'ЁЭCHЪБЃЌдђHH'НтЮіЪНЮЊЃК![]()
ЕБy=0ЪБЃЌ![]()
Ёрt=4
ЁпШєХзЮяЯпLЙигкЕуMЖдГЦЕФаТХзЮяЯпЮЊLЁфЃЌЧвЕуCЁЂHЕФЖдгІЕуЗжБ№ЮЊCЁфЃЌHЁфЃЛ
ЁрЕуC'(2tЃЌЉ3)ЃЌЕуH'(2tЉ2ЃЌ1)
ШєCH'ЁЭHH'ЃЌдђH'C2+H'H2=CH2ЃЌ
Ёр(2tЉ2Љ0)2+(3Љ1)2+(2tЉ2Љ2)2+(1+1)2=(0Љ2)2+(3+1)2ЃЌ
Ёрt=![]()
ШєCC'ЁЭCH'ЃЌдђH'C2+C'C2=C'H'2ЃЌ
Ёр(2tЉ2Љ0)2+(3Љ1)2+(2tЉ0)2+(3+3)2=(0Љ2)2+(3+1)2ЃЌ
ЁрЁїЃМ0ЃЌЗНГЬЮоНтЃЛ
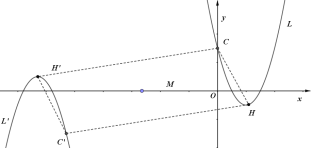
злЩЯЫљЪіЃКt=![]() Лђ4ЛђЉ6ЃЎ
Лђ4ЛђЉ6ЃЎ
ЙЪД№АИЮЊЃКt=![]() Лђ4ЛђЉ6ЃЎ
Лђ4ЛђЉ6ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк5ЁС5ЕФе§ЗНаЮЭјИёЃЌУПИіаЁе§ЗНаЮЕФБпГЄЖМЮЊ1ЃЌЯпЖЮABЕФЖЫЕуТфдкИёЕуЩЯЃЌвЊЧѓЛвЛИіЫФБпаЮЃЌЫљзїЕФЫФБпаЮЮЊжааФЖдГЦЭМаЮЃЌЭЌЪБТњзуЯТСавЊЧѓЃК
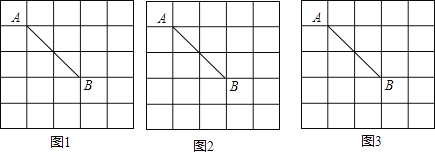
ЃЈ1ЃЉдкЭМ1жаЛГівдABЮЊвЛБпЕФЫФБпаЮЃЛ
ЃЈ2ЃЉЗжБ№дкЭМ2КЭЭМ3жаИїЛГівЛИівдABЮЊвЛЬѕЖдНЧЯпЕФЫФБпаЮЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
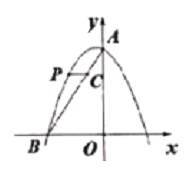
ЁОЬтФПЁПШчЭМЃЌЖўДЮКЏЪ§y=-x2+(n-1)x+3ЕФЭМЯёгыyжсНЛгкЕуAЃЌгыxжсЕФИКАыжсНЛгкЕуB(-2ЃЌ0)
(1)ЧѓЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
(2)ЕуPЪЧетИіЖўДЮКЏЪ§ЭМЯёдкЕкЖўЯѓЯоФкЕФвЛЯпЃЌЙ§ЕуPзїyжсЕФДЙЯпгыЯпЖЮABНЛгкЕуCЃЌЧѓЯпЖЮPCГЄЖШЕФзюДѓжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
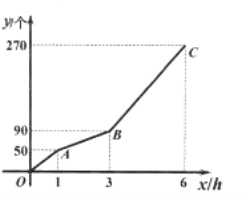
ЁОЬтФПЁПМзЁЂввСНЬЈЛњЦїЙВЭЌМгЙЄвЛХњСуМўЃЌвЛЙВгУСЫ![]() аЁЪБЃЎдкМгЙЄЙ§ГЬжаввЛњЦївђЙЪеЯЭЃжЙЙЄзїЃЌХХГ§ЙЪеЯКѓЃЌввЛњЦїЬсИпСЫЙЄзїаЇТЪЧвБЃГжВЛБфЃЌМЬајМгЙЄЃЎМзЛњЦїдкМгЙЄЙ§ГЬжаЙЄзїаЇТЪБЃГжВЛБфЃЎМзЁЂввСНЬЈЛњЦїМгЙЄСуМўЕФзмЪ§
аЁЪБЃЎдкМгЙЄЙ§ГЬжаввЛњЦївђЙЪеЯЭЃжЙЙЄзїЃЌХХГ§ЙЪеЯКѓЃЌввЛњЦїЬсИпСЫЙЄзїаЇТЪЧвБЃГжВЛБфЃЌМЬајМгЙЄЃЎМзЛњЦїдкМгЙЄЙ§ГЬжаЙЄзїаЇТЪБЃГжВЛБфЃЎМзЁЂввСНЬЈЛњЦїМгЙЄСуМўЕФзмЪ§![]() ЃЈИіЃЉгыМзМгЙЄЪБМф
ЃЈИіЃЉгыМзМгЙЄЪБМф![]() жЎМфЕФКЏЪ§ЭМЯѓЮЊелЯп
жЎМфЕФКЏЪ§ЭМЯѓЮЊелЯп![]() ЃЌШчЭМЫљЪОЃЎ
ЃЌШчЭМЫљЪОЃЎ
ЃЈ1ЃЉетХњСуМўвЛЙВгаЁЁ ЁЁИіЃЌМзЛњЦїУПаЁЪБМгЙЄЁЁ ЁЁИіСуМўЃЌввЛњЦїХХГ§ЙЪеЯКѓУПаЁЪБМгЙЄЁЁ ЁЁИіСуМўЃЛ
ЃЈ2ЃЉЕБ![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() гы
гы![]() жЎМфЕФКЏЪ§НтЮіЪНЃЛ
жЎМфЕФКЏЪ§НтЮіЪНЃЛ
ЃЈ3ЃЉдкећИіМгЙЄЙ§ГЬжаЃЌМзМгЙЄЖрГЄЪБМфЪБЃЌМзгыввМгЙЄЕФСуМўИіЪ§ЯрЕШЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
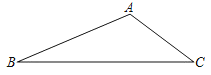
ЁОЬтФПЁПШчЭМЃЌЯпЖЮBCКЭЖЏЕуAЙЙГЩЁїABCЃЌЁЯBAC=120ЁуЃЌBC=3ЃЌдђЁїABCжмГЄЕФзюДѓжЕ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП5дТ13ШеЃЌжмНмТз2017ЁАЕиБэзюЧПЁБЪРНчбВЛибнГЊЛсдкАТЬхжааФЪЂДѓОйааЃЌ1КХбВТпдБДгЮшЬЈзпЭљПДЬЈЃЌ2КХбВТпКХДгПДЬЈзпЭљЮшЬЈЃЌСНШЫЭЌЪБГіЗЂЃЌЗжБ№вдИїздЕФЫйЖШдкЮшЬЈгыПДЬЈМфдШЫйзпЖЏЃЌГіЗЂ1ЗжжгКѓЃЌ1КХбВТпдБЗЂЯжЖдНВЛњвХЭќдкГіЗЂЕиЃЌБуСЂМДЗЕЛиГіЗЂЕиЃЌФУЕНЖдНВЛњКѓЃЈШЁЖдНВЛњЪБМфВЛМЦЃЉСЂМДдйДгЮшЬЈзпЭљПДЬЈЃЌНсЙћ1КХбВТпдБЯШЕНДяПДЬЈЃЌ2КХбВТпдБМЬајзпЕНЮшЬЈЃЌЩш2КХбВТпдБЕФааЪЛЪБМфЮЊxЃЈminЃЉЃЌСНШЫжЎМфЕФОрРыЮЊyЃЈmЃЉЃЌyгыxЕФКЏЪ§ЭМЯѓШчЭМЫљЪОЃЌдђЕБ1КХбВТпдБЕНДяПДЬЈЪБЃЌ2КХбВТпдБРыЮшЬЈЕФОрРыЪЧ________УзЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЃКжБЯп![]() НЛxжсгкЕуAЃЌНЛyжсгкЕуBЃЌХзЮяЯпy=ax2+bx+cОЙ§AЁЂBЁЂCЃЈ1ЃЌ0ЃЉШ§ЕуЃЎ
НЛxжсгкЕуAЃЌНЛyжсгкЕуBЃЌХзЮяЯпy=ax2+bx+cОЙ§AЁЂBЁЂCЃЈ1ЃЌ0ЃЉШ§ЕуЃЎ
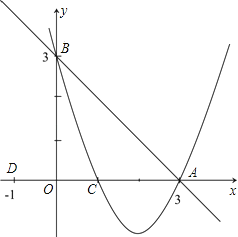
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШєЕуDЕФзјБъЮЊЃЈ-1ЃЌ0ЃЉЃЌдкжБЯп![]() ЩЯгавЛЕуP,ЪЙІЄABOгыІЄADPЯрЫЦЃЌЧѓГіЕуPЕФзјБъЃЛ
ЩЯгавЛЕуP,ЪЙІЄABOгыІЄADPЯрЫЦЃЌЧѓГіЕуPЕФзјБъЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌдкxжсЯТЗНЕФХзЮяЯпЩЯЃЌЪЧЗёДцдкЕуEЃЌЪЙІЄADEЕФУцЛ§ЕШгкЫФБпаЮAPCEЕФУцЛ§ЃПШчЙћДцдкЃЌЧыЧѓГіЕуEЕФзјБъЃЛШчЙћВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯBACЃН90ЁуЃЌЁЯBЃН60ЁуЃЌABЃН2ЃЎADЁЭBCгкDЃЎEЮЊБпBCЩЯЕФвЛИіЃЈВЛгыBЁЂCжиКЯЃЉЕуЃЌЧвAEЁЭEFгкEЃЌЁЯEAFЃНЁЯBЃЌAFЯрНЛгкЕуFЃЎ
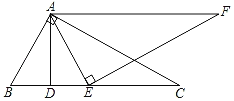
ЃЈ1ЃЉЬюПеЃКACЃН_____ЃЛЁЯFЃН______ЃЎ
ЃЈ2ЃЉЕБBDЃНDEЪБЃЌжЄУїЃКЁїABCЁеЁїEAFЃЎ
ЃЈ3ЃЉЁїEAFУцЛ§ЕФзюаЁжЕЪЧ____ЃЎ
ЃЈ4ЃЉЕБЁїEAFЕФФкаФдкЁїABCЕФЭтВПЪБЃЌжБНгаДГіAEЕФЗЖЮЇ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкОиаЮABCDжаЃЌABЃН2ЃЌADЃН![]() ЃЌЕуMЮЊABЕФжаЕуЃЌЕуNЮЊADБпЩЯЕФвЛЖЏЕуЃЌНЋЁїAMNбиMNелЕўЃЌЕуAТфдкЕуPДІЃЌЕБЕуPдкОиаЮABCDЕФЖдНЧЯпЩЯЪБЃЌANЕФГЄЖШЮЊ_____ЃЎ
ЃЌЕуMЮЊABЕФжаЕуЃЌЕуNЮЊADБпЩЯЕФвЛЖЏЕуЃЌНЋЁїAMNбиMNелЕўЃЌЕуAТфдкЕуPДІЃЌЕБЕуPдкОиаЮABCDЕФЖдНЧЯпЩЯЪБЃЌANЕФГЄЖШЮЊ_____ЃЎ
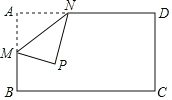
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com