
 如图是阜阳生态园欧阳修会老堂的圆弧形门,这个圆弧形门所在的圆与水平地面是相切的,AB=CD=20cm,BD=200cm,且AB,CD与水平地面都是垂直的,求这个圆弧形门的最高点离地面的高度.
如图是阜阳生态园欧阳修会老堂的圆弧形门,这个圆弧形门所在的圆与水平地面是相切的,AB=CD=20cm,BD=200cm,且AB,CD与水平地面都是垂直的,求这个圆弧形门的最高点离地面的高度. 分析 连接OF,交AC于点E,设圆O的半径为R,根据勾股定理列出方程,解方程即可.
解答 解:连接OF,交AC于点E,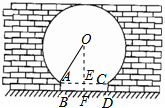
∵BD是⊙O的切线,
∴OF⊥BD,
∵四边形ABDC是矩形,
∴AD∥BD,
∴OE⊥AC,EF=AB,
设圆O的半径为R,在Rt△AOE中,AE=$\frac{AC}{2}$=$\frac{BD}{2}$=100,
OE=R-AB=R-20,
∵AE2+OE2=OA2,
∴1002+(R-20)2=R2,
解得,R=260.
260×2=520(cm).
答:这个圆弧形门的最高点离地面的高度为520cm.
点评 本题考查的是垂径定理的应用,掌握平分弦(不是直径)的直径垂直于弦是解题的关键,注意勾股定理的灵活运用.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:选择题
| A. | x2-4x+3=0 | B. | x2+3x+4=0 | C. | x2+4x-3=0 | D. | x2+3x-4=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在数学实践课中,小明为了测量学校旗杆CD的高度,在地面A处放置高度为1.5米的测角仪AB,测得旗杆顶端D的仰角为32°,AC为22米,则旗杆CD的高度约为15.1米.(结果精确到0.1米.参考数据:sin32°=0.53,cos32°=0.85,tan32°=0.62)
如图,在数学实践课中,小明为了测量学校旗杆CD的高度,在地面A处放置高度为1.5米的测角仪AB,测得旗杆顶端D的仰角为32°,AC为22米,则旗杆CD的高度约为15.1米.(结果精确到0.1米.参考数据:sin32°=0.53,cos32°=0.85,tan32°=0.62)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 条形统计图 | B. | 扇形统计图 | C. | 折线统计图 | D. | 以上均可以 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8.
如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a+b | B. | abc | C. | 1000a+10b+c | D. | 100c+10b+a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com