
如图,在平面直角坐标系中,直线 y=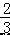 x﹣
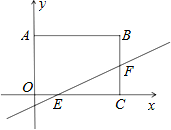
x﹣ 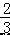 与矩形 ABCO 的边 OC、BC 分别交于点 E、F,已 知 OA=3,OC=4,则△CEF 的面积是( )
与矩形 ABCO 的边 OC、BC 分别交于点 E、F,已 知 OA=3,OC=4,则△CEF 的面积是( )
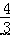 A.6 B.3 C.12 D.
A.6 B.3 C.12 D.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
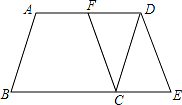
如图,在▱ABCD 中,F 是 AD 的中点,延长 BC 到点 E,使 CE=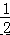 BC,连接 DE,CF.
BC,连接 DE,CF.
(1)求证:四边形 CEDF 是平行四边形; 若 AB=4,AD=6,∠B=60°,求 DE 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
若 x,y 为实数,且满足|x﹣3|+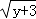 =0.
=0.
(1)如果实数 x,y 对应为平面直角坐标系上的点 A(x,y),则点 A 在第几象限? 求( 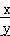 )2015 的值?
)2015 的值?
查看答案和解析>>
科目:初中数学 来源: 题型:
某商场代销甲、乙两种商品,其中甲种商品的进价为 120 元/件,售件为 130 元/件,乙种商品的
进价为 100 元/件,售件为 150 元/件.
(1)若商场用 36000 元购进这两种商品,销售完后可获得利润 6000 元,则该商场购进甲、乙两种 商品各多少件?
若商场要购进这两种商品共 200 件,设购进甲种商品 x 件,销售后获得的利润为 W 元,试写出利润 W(元)与 x(件)函数关系式(不要求写出自变量 x 的取值范围);并指出购进甲种商品件数 x 逐 渐增加时,利润 W 是增加还是减少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com