
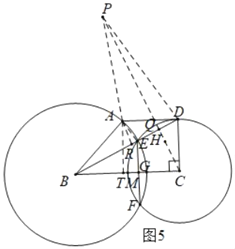
����Ŀ����ͼ��������ABCD�У�AD��BC����C=90�㣬DC=5����CDΪ�뾶�ġ�C����ABΪ�뾶�ġ�B�ཻ�ڵ�E��F���ҵ�E��BD�ϣ�����EF��BC�ڵ�G��
��1����BC���C�ཻ�ڵ�M����BM=ADʱ�����B�İ뾶��
��2����BC=x��EF=y����y����x�ĺ�����ϵʽ����д�����Ķ�����
��3����BC=10ʱ����PΪƽ����һ�㣬����P���C�ཻ�ڵ�D��E������A��E��P��DΪ������ı��������Σ���ֱ��д����P�����������������У�

���𰸡���1��![]() ����2��
����2��![]() ����3����
����3����![]() ������29��8
������29��8![]() ����
����
�ۡ�P�����Ϊ![]() ��
��
����������������1���������DM�ij�����֤���ı���ABMD��ƽ���ı��μ��ɽ�����⣻
��2����ͼ2�У�����C��CH��BD������Ϊ��H��������x��ʾBE�ij����ٸ���EG��BEsin��DBC��![]() ����⼴�ɣ�
����⼴�ɣ�
��3�����������ηֱ���⼴�ɽ�����⣻
��⣺��1����ͼ1�У�����DM��
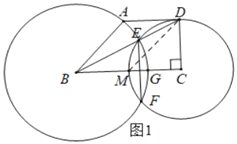
��Rt��DCM��![]() ��
��
��AD��BC BM=AD��
���ı���ABMDΪƽ���ı��Σ�
��AB=DM=![]() ��
��
����B�İ뾶Ϊ![]() ��
��
��2����ͼ2�У�����C��CH��BD������Ϊ��H��
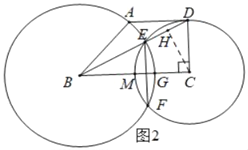
��Rt��BCD��![]() ��
��
��![]() ��
��
�ɵá�DCH=��DBC��
��![]() ��
��
��Rt��DCH��DH=DC![]() sin��DCH=
sin��DCH=![]() ��
��
��CH��BD��
��DE=2DH=![]() ��
��
��![]()
�ߡ�C���B�ཻ�ڵ�E��F��
��EF=2EG��BC��EF��
��Rt��EBG��
![]() ��
��
��![]() (x>
(x>![]() )��
)��
��3������ͼ3�У���PE��ADʱ����PC��DE��H����CH��ֱƽ���߶�DE��
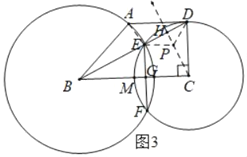
��Rt��BCD��BD=![]() ��CH=
��CH=![]() ��
��
DH=![]() ��
��
��EH=DH=![]() ��
��
��AD��BC��PE��AD��
��PE��BC��
���HEP=��HBC��
��cos��HEP=cos��CBD��
��![]() ��
��
��![]() ��
��
��PE=![]() ��
��
���P�����Ϊ![]() �У�
�У�
����ͼ4�У���AP��DEʱ����AT��BC��T����AD��PC��Q��BD��PC��H��
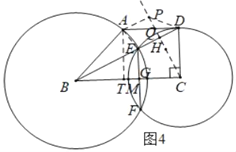
�ɢٿ�֪��DE=2![]() ��BE=BA=3
��BE=BA=3![]() ��AT=CD=5��
��AT=CD=5��
��Rt��ABT��BT=![]() ��
��
��AD=CT=10��2![]() ��
��
����DQH�ס�BDC���ɵ�DQ=![]() ��QH=
��QH=![]() ��
��
��AQ=AD��DQ=![]() ��2
��2![]() ��
��
����APQ�ס�DHQ���ɵ�PQ=![]() ��2��
��2��
��Rt��PDH��PD2=DH2+PH2=29��8![]() ��
��
���P�����Ϊ��29��8![]() ���У�
����
����ͼ5�У���DP��AEʱ����AR��BD��R��
����ADR�ס�DBC��
��![]() ��
��
��AR=2![]() ��2��DR=4
��2��DR=4![]() ��4��
��4��
��ER=DR��DE=2![]() ��4��
��4��
��Rt��ARE��AE=![]() ��
��
��AE��DP��
���AER=��PDQ��
��cos��AER=cos��PDH��
��![]() ��
��
��PD=![]() ��
��
���P�����Ϊ![]() ��
��


 ��ѧ�����ϵ�д�
��ѧ�����ϵ�д� �·Ƿ��̸����100��ϵ�д�
�·Ƿ��̸����100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У���O�DZ�BC���е㣬����DO���ӳ�����AB�ӳ����ڵ�E������BD��EC��
(1)��֤���ı���BECD��ƽ���ı��Σ�
(2)����A��50������BOD��100��ʱ���ж��ı���BECD����״����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB=90�㣬AB=10��sinA=![]() ��CDΪAB���ϵ����ߣ��Ե�BΪԲ�ģ�rΪ�뾶����B�������B������CD����ֻ��һ�������㣬��ô��B�İ뾶r��ȡֵ��ΧΪ_____��
��CDΪAB���ϵ����ߣ��Ե�BΪԲ�ģ�rΪ�뾶����B�������B������CD����ֻ��һ�������㣬��ô��B�İ뾶r��ȡֵ��ΧΪ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
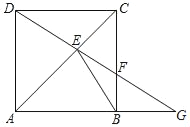
����Ŀ����ͼ���ı���ABCD�Ǿ��Σ�E�ǶԽ���AC�ϵ�һ�㣬EB=ED�ҡ�ABE=��ADE��
��1����֤���ı���ABCD�������Σ�
��2���ӳ�DE��BC�ڵ�F����AB���ӳ����ڵ�G����֤��EFAG=BCBE��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=ax2+bx+c��x�ύ�ڵ�A(1��0)��B(3��0)���ҹ���C(0��-3).
(1)�������ߵĽ���ʽ�Ͷ������ꣻ
(2)����д��һ��ƽ�Ƶķ�����ʹƽ�ƺ������ߵĶ�������ֱ��y=-x�ϣ���д��ƽ�ƺ������ߵĽ���ʽ.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������С��ϵ�ж���ȷ���ǣ�������
A. 0��|��10| B. ������![]() ������|��
������|��![]() | C. |��3|��|+3| D. ��1����0.01
| C. |��3|��|+3| D. ��1����0.01
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
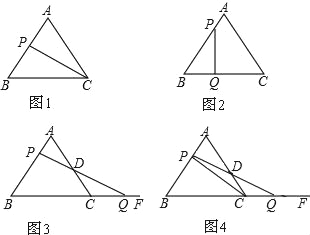
����Ŀ����֪����ABC�DZ߳�3cm�ĵȱ������Σ�����P��1cm/s���ٶȴӵ�A���������߶�AB���B�˶���
��1����ͼ1�����P���˶�ʱ��Ϊt��s������ôt���� ����s��ʱ����PBC��ֱ�������Σ�
��2����ͼ2������һ����Q�ӵ�B���������߶�BC���C�˶����������P��Q����1cm/s���ٶ�ͬʱ���������˶�ʱ��Ϊt��s������ôtΪ��ֵʱ����PBQ��ֱ�������Σ�
��3����ͼ3������һ����Q�ӵ�C������������BC�����˶�������PQ��AC��D���������P��Q����1cm/s���ٶ�ͬʱ���������˶�ʱ��Ϊt��s������ôtΪ��ֵʱ����DCQ�ǵ��������Σ�
��4����ͼ4������һ����Q�ӵ�C������������BC�����˶�������PQ��AC��D������PC���������P��Q����1cm/s���ٶ�ͬʱ������������룺�ڵ�P��Q���˶������У���PCD����QCD�������ʲô��ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
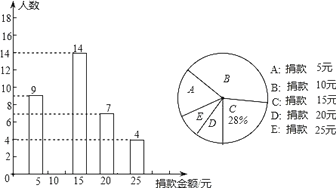
����Ŀ��ijУ���꼶ȫ��ͬѧ�μ���ij�������������˲���ͬѧ�������ͳ����ͼ��ʾ
(1)���ι����ѧ��____�ˣ���������ͼ����������
(2)������������_____��ƽ������_____��
(3)�ڰ��꼶700��ѧ���У����20Ԫ������(��20Ԫ)��ѧ�������ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵�����10̨A�ͺ�20̨B�͵��Ե�����Ϊ4000Ԫ������20̨A�ͺ�10̨B�͵��Ե�����Ϊ3500Ԫ.
��1����ÿ̨A�͵��Ժ�B�͵��Ե���������
��2�����̵�ƻ�һ�ι��������ͺŵĵ��Թ�100̨������B�͵��ԵĽ�����������A�͵��Ե�2�����蹺��A�͵���x̨����100̨���Ե�����������ΪyԪ.
����y����x�ĺ�����ϵʽ��
�ڸ��̵깺��A�͡�B�͵��Ը�����̨������ʹ�������������
��3��ʵ�ʽ���ʱ�����Ҷ�A�͵��Գ������µ�m(0<m<100)Ԫ�������̵�����A�͵���70̨.���̵걣�����ֵ��Ե��ۼ۲��䣬�������������Ϣ��(2)����������Ƴ�ʹ��100̨�����������������Ľ�������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com