【题目】下列有理数大小关系判断正确的是（ ）
A. 0＞|﹣10| B. ﹣（﹣
）＞﹣|﹣
| C. |﹣3|＜|+3| D. ﹣1＞﹣0.01
【答案】B
【解析】
A.首先求出|﹣10|=10，然后根据有理数大小比较的方法判断即可;B.首先判断出﹣（﹣
）=，﹣|﹣
|=﹣，然后根据有理数大小比较的方法判断即可;C.首先判断出|﹣3|=3，|+3|=3，然后根据有理数大小比较的方法判断即可;D.两个负数，绝对值大的其值反而小，据此判断即可．
∵|﹣10|=10，0＜10，
∴0＜|﹣10|，
∴选项A不正确；
∵﹣（﹣）=，﹣|﹣|=﹣，＞﹣，
∴﹣（﹣）＞﹣|﹣|，
∴选项B正确；
∵|﹣3|=3，|+3|=3，
∴|﹣3|=|+3|，
∴选项C不正确；
∵|﹣1|=1，|﹣0.01|=0.01，1＞0.01，
∴﹣1＜﹣0.01，
∴选项D不正确．
故选：B．
新课标阶梯阅读训练系列答案
口算心算速算应用题系列答案科目：初中数学 来源： 题型：
【题目】某灯具厂计划一天生产300盏景观灯，但由于各种原因，实际每天生产景观灯盏数与计划每天生产景观灯盏数相比有出入.下表是某周的生产情况（增产记为正，减产记为负）：
⑴求该厂这周实际生产景观灯的盏数；
⑵求该厂这周产量最多的一天比产量最少的一天多生产景观灯的盏数；
⑶该厂实出售该中灯，每盏可获得40元的利润，若把本周生产的所有灯全部销售掉，可赚多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读第①小题的计算方法，再计算第②小题．
①–5
+（–9
）+17
+（–3
）
解：原式=[（–5）+（–）]+[（–9）+（–）]+（17+）+[（–3+（–）]
=[（–5）+（–9）+（–3）+17]+[（–）+（–）+（–）+]
=0+（–1
）
=–1．
上述这种方法叫做拆项法．灵活运用加法的交换律、结合律可使运算简便．
②仿照上面的方法计算：（﹣2000）+（﹣1999）+4000+（﹣1）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】“今有善行者行一百步，不善行者行六十步”（出自《九章算术》）意思是：同样时间段内，走路快的人能走100步，走路慢的人只能走60步，假定两者步长相等，据此回答以下问题：
（1）今不善行者先行一百步，善行者追之，不善行者再行六百步，问孰至于前，两者几何步隔之？即：走路慢的人先走100步，走路快的人开始追赶，当走路慢的人再走600步时，请问谁在前面，两人相隔多少步？
（2）今不善行者先行两百步，善行者追之，问几何步及之？即：走路慢的人先走200步，请问走路快的人走多少步才能追上走路慢的人？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，有一条直线l：
与x轴、y轴分别交于点M、N，一个高为3的等边三角形ABC，边BC在x轴上，将此三角形沿着x轴的正方向平移．
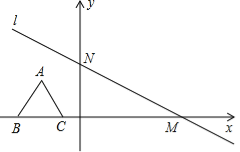
（1）在平移过程中，得到△A1B1C1，此时顶点A1恰落在直线l上，写出A1点的坐标 ；
（2）继续向右平移，得到△A2B2C2，此时它的外心P恰好落在直线l上，求P点的坐标；
（3）在直线l上是否存在这样的点，与（2）中的A2、B2、C2任意两点能同时构成三个等腰三角形？如果存在，求出点的坐标；如果不存在，说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】二次函数y=ax2+bx+c（a≠0）的图象经过点A（3，0），B（2，﹣3），并且以x=1为对称轴．
（1）求此函数的解析式；
（2）作出二次函数的大致图象；
（3）在对称轴x=1上是否存在一点P，使△PAB中PA=PB？若存在，求出P点的坐标；若不存在，说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】将一张长方形的纸对折，如图所示可得到一条折痕（图中虚线），继续对折，对折时每次折痕与上次的折痕保持平行，连续对折三次后，可以得7条折痕，那么对折四次可以得到 条折痕，如果对折
次，可以得到 条折痕．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
