
【题目】如图,在Rt△ABC中,∠ACB=90°,AB=10,sinA=![]() ,CD为AB边上的中线,以点B为圆心,r为半径作⊙B.如果⊙B与中线CD有且只有一个公共点,那么⊙B的半径r的取值范围为_____.
,CD为AB边上的中线,以点B为圆心,r为半径作⊙B.如果⊙B与中线CD有且只有一个公共点,那么⊙B的半径r的取值范围为_____.

 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
【题目】某校八年级全体同学参加了某项捐款活动,随机抽查了部分同学捐款的情况统计如图所示
(1)本次共抽查学生____人,并将条形图补充完整;
(2)捐款金额的众数是_____,平均数是_____;
(3)在八年级700名学生中,捐款20元及以上(含20元)的学生估计有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
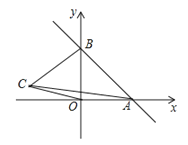
【题目】如图,一次函数y=kx+b的图象分别与x轴,y轴的正半轴分別交于点A,B,AB=2![]() ,∠OAB=45°
,∠OAB=45°
(1)求一次函数的解析式;
(2)如果在第二象限内有一点C(a,![]() );试用含有a的代数式表示四边形ABCO的面积,并求出当△ABC的面积与△ABO的面积相等时a的值;
);试用含有a的代数式表示四边形ABCO的面积,并求出当△ABC的面积与△ABO的面积相等时a的值;
(3)在x轴上,是否存在点P,使△PAB为等腰三角形?若存在,请直接写出所有符合条件的点P坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B,C三点在数轴上,点A表示的数为-10,点B表示的数为14,点C到点A和点B之间的距离相等.
![]()
(1)求A,B两点之间的距离;
(2)求C点对应的数;
(3)甲、乙分别从A,B两点同时相向运动,甲的速度是1个单位长度/s,乙的速度是2个单位长度/s,求相遇点D对应的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习绝对值后,我们知道,|a|表示数a在数轴上的对应点与原点的距离.如:|5|表示5在数轴上的对应点到原点的距离.而|5|=|5﹣0|,即|5﹣0|也可理解为5、0在数轴上对应的两点之间的距离.类似的,|5-3|表示5与3之差的绝对值,也可理解为5与3两数在数轴上所对应的两点之间的距离.如|x-3|的几何意义是数轴上表示有理数3的点与表示数x的点之间的距离,一般地,点A、B在数轴上分别表示数a、b,那么A、B之间的距离可表示为|a﹣b|.
请根据绝对值的意义并结合数轴解答下列问题:
![]()
(1)数轴上表示2和3的两点之间的距离是 ;数轴上表示数a的点与表示﹣2的点之间的距离表示为 ;
(2)数轴上点P表示的数是2,P、Q两点的距离为3,则点Q表示的数是 ;
(3)数轴上有一个点表示数a,则|a+1|+|a-3|+|a+8|的最小值为 ;
(4)a、b、c、d在数轴上的位置如下图所示,若|a-d|=12,|b-d|=7,|a-c|=9,则|b-c|等于 .
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在等腰直角三角形中,AB=AC,点D是斜边BC上的中点,点E、F分别为AB,AC上的点,且DE⊥DF。(1)若设![]() ,
,![]() ,满足
,满足![]() .
.
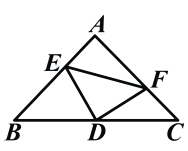
(1)求BE及CF的长。
(2)求证:![]() 。
。
(3)在(1)的条件下,求△DEF的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着信息技术的高速发展,计算机技术已是每位学生应该掌握的基本技能.为了提高学生对计算机的兴趣,老师把甲、乙两组各有10名学生,进行电脑汉字输入速度比赛,各组参赛学生每分钟输入汉字个数统计如下表:
输入汉字(个) | 132 | 133 | 134 | 135 | 136 | 137 |
甲组人数(人) | 1 | 0 | 1 | 5 | 2 | 1 |
乙组人数(人) | 0 | 1 | 4 | 1 | 2 | 2 |
(1)请你填写下表中甲班同学的相关数据.
组 | 众数 | 中位数 | 平均数( | 方差( |
甲组 | ||||
乙组 | 134 | 134.5 | 135 | 1.8 |
(2)若每分钟输入汉字个数136及以上为优秀,则从优秀人数的角度评价甲、乙两组哪个成绩更好一些?
(3)请你根据所学的统计知识,从不同角度评价甲、乙两组学生的比赛成绩(至少从两个角度进行评价).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD∥BC,∠C=90°,DC=5,以CD为半径的⊙C与以AB为半径的⊙B相交于点E、F,且点E在BD上,联结EF交BC于点G.
(1)设BC与⊙C相交于点M,当BM=AD时,求⊙B的半径;
(2)设BC=x,EF=y,求y关于x的函数关系式,并写出它的定义域;
(3)当BC=10时,点P为平面内一点,若⊙P与⊙C相交于点D、E,且以A、E、P、D为顶点的四边形是梯形,请直接写出⊙P的面积.(结果保留π)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(11·湖州)(本小题10分)
如图,已知E、F分别是□ABCD的边BC、AD上的点,且BE=DF。
⑴求证:四边形AECF是平行四边形;
⑵若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com