
【题目】随着信息技术的高速发展,计算机技术已是每位学生应该掌握的基本技能.为了提高学生对计算机的兴趣,老师把甲、乙两组各有10名学生,进行电脑汉字输入速度比赛,各组参赛学生每分钟输入汉字个数统计如下表:
输入汉字(个) | 132 | 133 | 134 | 135 | 136 | 137 |
甲组人数(人) | 1 | 0 | 1 | 5 | 2 | 1 |
乙组人数(人) | 0 | 1 | 4 | 1 | 2 | 2 |
(1)请你填写下表中甲班同学的相关数据.
组 | 众数 | 中位数 | 平均数( | 方差( |
甲组 | ||||
乙组 | 134 | 134.5 | 135 | 1.8 |
(2)若每分钟输入汉字个数136及以上为优秀,则从优秀人数的角度评价甲、乙两组哪个成绩更好一些?
(3)请你根据所学的统计知识,从不同角度评价甲、乙两组学生的比赛成绩(至少从两个角度进行评价).
【答案】(1)填写表格见解析;(2)乙组成绩更好一些;(3)①从众数看,甲班众数成绩优于乙班;②从中位数看,甲班每分钟输入135字以上的人数比乙班多;③从平均数看,两班同学输入的总字数一样,成绩相当;④从方差看,甲班成绩波动小,比较稳定;⑤从最好成绩看,乙班成绩优于甲班.(至少从两个角度进行评价).
【解析】
(1)根据众数、中位数、平均数以及方差的计算公式分别进行解答即可;
(2)根据表中给出的数据,得出甲组优秀的人数有3人,乙组优秀的人数有4人,从而得出乙组成绩更好一些;
(3)从中位数看,甲组每分钟输入135字以上的人数比乙组多;从方差看,S2甲<S2乙;甲组成绩波动小,比较稳定.
解:(1)如下表:
组 | 众数 | 中位数 | 平均数( | 方差( |
甲组 | 135 | 135 | 135 | 1.6 |
乙组 | 134 | 134.5 | 135 | 1.8 |
(2)∵每分钟输入汉字个数136及以上的甲组人数有3人,乙组有4人
∴乙组成绩更好一些
(3)①从众数看,甲班每分钟输入135字的人数最多,乙班每分钟输入134字的人数最多,甲班众数成绩优于乙班;
②从中位数看,甲班每分钟输入135字以上的人数比乙班多;
③从平均数看,两班同学输入的总字数一样,成绩相当;
④从方差看,甲的方差小于乙的方差,则甲班成绩波动小,比较稳定;
⑤从最好成绩看,乙班速度最快的选手比甲班多1人,若比较前3~4名选手的成绩,则乙班成绩优于甲班.(至少从两个角度进行评价).


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:
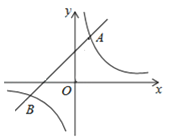
【题目】如图,已知在平面直角坐标系中, ![]() 是坐标原点,点A(2,5)在反比例函数
是坐标原点,点A(2,5)在反比例函数![]() 的图象上.一次函数
的图象上.一次函数![]() 的图象过点A,且与反比例函数图象的另一交点为B.
的图象过点A,且与反比例函数图象的另一交点为B.
(1)求![]() 和
和![]() 的值;
的值;
(2)设反比例函数值为![]() ,一次函数值为
,一次函数值为![]() ,求
,求![]() 时
时![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AB=10,sinA=![]() ,CD为AB边上的中线,以点B为圆心,r为半径作⊙B.如果⊙B与中线CD有且只有一个公共点,那么⊙B的半径r的取值范围为_____.
,CD为AB边上的中线,以点B为圆心,r为半径作⊙B.如果⊙B与中线CD有且只有一个公共点,那么⊙B的半径r的取值范围为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】郊区某中学学霸父母只要有时间就陪孩子一起完成家庭作业,在某天晚上,勤芬准备完成作业时:化简(![]() x2+7x+6)﹣(7x+8x2﹣4).发现系数“
x2+7x+6)﹣(7x+8x2﹣4).发现系数“![]() ”印刷不清楚.
”印刷不清楚.
(1)她把“![]() ”猜成3,请你化简:(3x2+7x+6)﹣(7x+8x2﹣4);
”猜成3,请你化简:(3x2+7x+6)﹣(7x+8x2﹣4);
(2)爸爸说:“你猜错了,我看了标准答案的结果是常数.”请你通过计算说明来帮助勤芬得到原题中“![]() ”是几.
”是几.
查看答案和解析>>
科目:初中数学 来源: 题型:
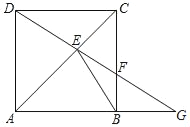
【题目】如图,四边形ABCD是矩形,E是对角线AC上的一点,EB=ED且∠ABE=∠ADE.
(1)求证:四边形ABCD是正方形;
(2)延长DE交BC于点F,交AB的延长线于点G,求证:EFAG=BCBE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c与x轴交于点A(1,0),B(3,0),且过点C(0,-3).
(1)求抛物线的解析式和顶点坐标;
(2)请你写出一种平移的方法,使平移后抛物线的顶点落在直线y=-x上,并写出平移后抛物线的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
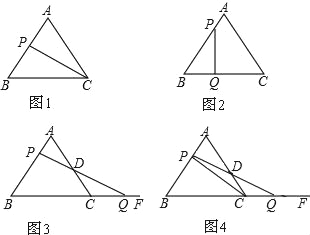
【题目】已知,△ABC是边长3cm的等边三角形.动点P以1cm/s的速度从点A出发,沿线段AB向点B运动.
(1)如图1,设点P的运动时间为t(s),那么t= (s)时,△PBC是直角三角形;
(2)如图2,若另一动点Q从点B出发,沿线段BC向点C运动,如果动点P、Q都以1cm/s的速度同时出发.设运动时间为t(s),那么t为何值时,△PBQ是直角三角形?
(3)如图3,若另一动点Q从点C出发,沿射线BC方向运动.连接PQ交AC于D.如果动点P、Q都以1cm/s的速度同时出发.设运动时间为t(s),那么t为何值时,△DCQ是等腰三角形?
(4)如图4,若另一动点Q从点C出发,沿射线BC方向运动.连接PQ交AC于D,连接PC.如果动点P、Q都以1cm/s的速度同时出发.请你猜想:在点P、Q的运动过程中,△PCD和△QCD的面积有什么关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知 a b , a 与b 两个数在数轴上对应的点分别为点 A 、点 B ,求 A 、 B 两点之间的距离.
(探索)
小明利用绝对值的概念,结合数轴,进行探索:
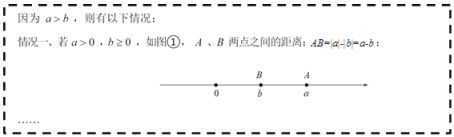
(1)补全小明的探索
(应用)
(2)若点C 对应的数c ,数轴上点C 到A、B 两点的距离相等,求c .(用含a、b 的代数式表示)
(3)若点 D对应的数 d ,数轴上点 D 到 A 的距离是点 D 到 B 的距离的nn 0 倍,请探索 n 的取值范围与点 D 个数的关系,并直接写出a、b 、d、n 的关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com