
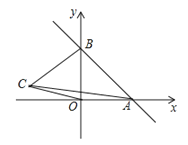
ЁОЬтФПЁПШчЭМЃЌвЛДЮКЏЪ§y=kx+bЕФЭМЯѓЗжБ№гыxжсЃЌyжсЕФе§АыжсЗжeНЛгкЕуAЃЌBЃЌAB=2![]() ЃЌЁЯOAB=45Ёу
ЃЌЁЯOAB=45Ёу
ЃЈ1ЃЉЧѓвЛДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШчЙћдкЕкЖўЯѓЯоФкгавЛЕуC(aЃЌ![]() )ЃЛЪдгУКЌгаaЕФДњЪ§ЪНБэЪОЫФБпаЮABCOЕФУцЛ§ЃЌВЂЧѓГіЕБЁїABCЕФУцЛ§гыЁїABOЕФУцЛ§ЯрЕШЪБaЕФжЕЃЛ
)ЃЛЪдгУКЌгаaЕФДњЪ§ЪНБэЪОЫФБпаЮABCOЕФУцЛ§ЃЌВЂЧѓГіЕБЁїABCЕФУцЛ§гыЁїABOЕФУцЛ§ЯрЕШЪБaЕФжЕЃЛ
ЃЈ3ЃЉдкxжсЩЯЃЌЪЧЗёДцдкЕуPЃЌЪЙЁїPABЮЊЕШбќШ§НЧаЮЃПШєДцдкЃЌЧыжБНгаДГіЫљгаЗћКЯЬѕМўЕФЕуPзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉвЛДЮКЏЪ§НтЮіЪНЮЊy= -x+2 ЃЈ2ЃЉaЃН![]() ЃЈ3ЃЉДцдкЃЌТњзуЬѕМўЕФЕуPЕФзјБъЮЊЃЈ0ЃЌ0ЃЉЛђЃЈ22
ЃЈ3ЃЉДцдкЃЌТњзуЬѕМўЕФЕуPЕФзјБъЮЊЃЈ0ЃЌ0ЃЉЛђЃЈ22![]() ЃЌ0ЃЉЛђЃЈ2
ЃЌ0ЃЉЛђЃЈ2![]() +2ЃЌ0ЃЉЛђЃЈ-2ЃЌ0ЃЉЃЎ
+2ЃЌ0ЃЉЛђЃЈ-2ЃЌ0ЃЉЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЙДЙЩЖЈРэЧѓГіAЁЂBСНЕузјБъЃЌРћгУД§ЖЈЯЕЪ§ЗЈМДПЩНтОіЮЪЬтЃЛ
ЃЈ2ЃЉИљОнSЫФБпаЮABCD=SЁїAOB+SЁїBOCМЦЫуМДПЩЃЌСаГіЗНГЬМДПЩЧѓГіaЕФжЕЃЛ
ЃЈ3ЃЉЗжШ§жжЧщаЮЬжТлМДПЩНтОіЮЪЬтЃЛ
ЃЈ1ЃЉдкRtЁїABOжаЃЌЁЯOAB=45ЁуЃЌ
ЁрЁЯOBA=ЁЯOAB-ЁЯOAB=90Ёу-45Ёу=45Ёу
ЁрЁЯOBA=ЁЯOAB
ЁрOA=OB
ЁрOB2+OA2=AB2МДЃК2OB2=ЃЈ2![]() ЃЉ2ЃЌ
ЃЉ2ЃЌ
ЁрOB=OA=2
ЁрЕуAЃЈ2ЃЌ0ЃЉЃЌBЃЈ0ЃЌ2ЃЉЃЎ
Ёр![]()
НтЕУЃК![]()
ЁрвЛДЮКЏЪ§НтЮіЪНЮЊy= -x+2ЃЎ
ЃЈ2ЃЉШчЭМЃЌ
ЁпSЁїAOB=![]() ЁС2ЁС2=2ЃЌSЁїBOC=
ЁС2ЁС2=2ЃЌSЁїBOC=![]() ЁС2ЁС|a|= -aЃЌ
ЁС2ЁС|a|= -aЃЌ
ЁрSЫФБпаЮABCD=SЁїAOB+SЁїBOC=2-aЃЌ
ЁпSЁїABC=SЫФБпаЮABCO-SЁїAOC=2-a-![]() ЁС2ЁС
ЁС2ЁС![]() =
=![]() -aЃЌ
-aЃЌ
ЕБЁїABCЕФУцЛ§гыЁїABOУцЛ§ЯрЕШЪБЃЌ![]() aЃН2ЃЌНтЕУaЃН
aЃН2ЃЌНтЕУaЃН![]() ЃЎ
ЃЎ
ЃЈ3ЃЉдкxжсЩЯЃЌДцдкЕуPЃЌЪЙЁїPABЮЊЕШбќШ§НЧаЮ
ЂйЕБPA=PBЪБЃЌPЃЈ0ЃЌ0ЃЉЃЌ
ЂкЕБBP=BAЪБЃЌPЃЈ-2ЃЌ0ЃЉЃЌ
ЂлЕБAB=APЪБЃЌPЃЈ2-2![]() ЃЌ0ЃЉЛђЃЈ2+2
ЃЌ0ЃЉЛђЃЈ2+2![]() ЃЌ0ЃЉЃЌ
ЃЌ0ЃЉЃЌ
злЩЯЫљЪіЃЌТњзуЬѕМўЕФЕуPЕФзјБъЮЊЃЈ0ЃЌ0ЃЉЛђЃЈ22![]() ЃЌ0ЃЉЛђЃЈ2
ЃЌ0ЃЉЛђЃЈ2![]() +2ЃЌ0ЃЉЛђЃЈ-2ЃЌ0ЃЉЃЎ
+2ЃЌ0ЃЉЛђЃЈ-2ЃЌ0ЃЉЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ![]() жаЃЌ
жаЃЌ![]() Чв
Чв![]() ЪЧ
ЪЧ![]() ЕФжаЕу
ЕФжаЕу

ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮ![]() ЪЧЦНааЫФБпаЮЁЃ
ЪЧЦНааЫФБпаЮЁЃ
ЃЈ2ЃЉЧѓжЄЃКЫФБпаЮ![]() ЪЧСтаЮЁЃ
ЪЧСтаЮЁЃ
ЃЈ3ЃЉШчЙћ![]() ЪБЃЌЧѓЫФБпаЮADBEЕФУцЛ§
ЪБЃЌЧѓЫФБпаЮADBEЕФУцЛ§
ЃЈ4ЃЉЕБ![]() ЖШЪБЃЌЫФБпаЮ
ЖШЪБЃЌЫФБпаЮ![]() ЪЧе§ЗНаЮЃЈВЛжЄУїЃЉ
ЪЧе§ЗНаЮЃЈВЛжЄУїЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
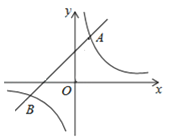
ЁОЬтФПЁПШчЭМЃЌвбжЊдкЦНУцжБНЧзјБъЯЕжаЃЌ ![]() ЪЧзјБъдЕуЃЌЕуAЃЈ2ЃЌ5ЃЉдкЗДБШР§КЏЪ§
ЪЧзјБъдЕуЃЌЕуAЃЈ2ЃЌ5ЃЉдкЗДБШР§КЏЪ§![]() ЕФЭМЯѓЩЯЃЎвЛДЮКЏЪ§
ЕФЭМЯѓЩЯЃЎвЛДЮКЏЪ§![]() ЕФЭМЯѓЙ§ЕуAЃЌЧвгыЗДБШР§КЏЪ§ЭМЯѓЕФСэвЛНЛЕуЮЊBЃЎ
ЕФЭМЯѓЙ§ЕуAЃЌЧвгыЗДБШР§КЏЪ§ЭМЯѓЕФСэвЛНЛЕуЮЊBЃЎ
ЃЈ1ЃЉЧѓ![]() КЭ
КЭ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉЩшЗДБШР§КЏЪ§жЕЮЊ![]() ЃЌвЛДЮКЏЪ§жЕЮЊ
ЃЌвЛДЮКЏЪ§жЕЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЪБ
ЪБ![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНааЫФБпаЮABCDжаЃЌЕуOЪЧБпBCЕФжаЕуЃЌСЌНгDOВЂбгГЄЃЌНЛABбгГЄЯпгкЕуEЃЌСЌНгBDЃЌECЃЎ
(1)ЧѓжЄЃКЫФБпаЮBECDЪЧЦНааЫФБпаЮЃЛ
(2)ЕБЁЯAЃН50ЁуЃЌЁЯBODЃН100ЁуЪБЃЌХаЖЯЫФБпаЮBECDЕФаЮзДЃЌВЂЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНёФъЫЎЙћДѓЗсЪеЃЌAЃЌBСНИіЫЎЙћЛљЕиЗжБ№ЪеЛёЫЎЙћ380МўЁЂ320МўЃЌЯжашАбетаЉЫЎЙћШЋВПдЫЭљМзЁЂввСНЯњЪлЕуЃЌДгAЛљЕидЫЭљМзЁЂввСНЯњЪлЕуЕФЗбгУЗжБ№ЮЊУПМў40дЊКЭ20дЊЃЌДгBЛљЕидЫЭљМзЁЂввСНЯњЪлЕуЕФЗбгУЗжБ№ЮЊУПМў15дЊКЭ30дЊЃЌЯжМзЯњЪлЕуашвЊЫЎЙћ400МўЃЌввЯњЪлЕуашвЊЫЎЙћ300МўЃЎ
ЃЈ1ЃЉЩшДгAЛљЕидЫЭљМзЯњЪлЕуЫЎЙћxМўЃЌзмдЫЗбЮЊWдЊЃЌЧыгУКЌxЕФДњЪ§ЪНБэЪОWЃЌВЂаДГіxЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉШєзмдЫЗбВЛГЌЙ§18300дЊЃЌЧвAЕидЫЭљМзЯњЪлЕуЕФЫЎЙћВЛЕЭгк200МўЃЌЪдШЗЖЈдЫЗбзюЕЭЕФдЫЪфЗНАИЃЌВЂЧѓГізюЕЭдЫЗбЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
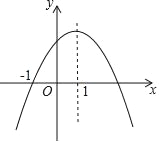
ЁОЬтФПЁПЖўДЮКЏЪ§y=ax2+bx+cЃЈaЃЌbЃЌcЮЊГЃЪ§ЃЌaЁй0ЃЉЕФЭМЯѓШчЭМЫљЪОЃЌЯТСаНсТлЃКЂйabcЃМ0ЃЛЂк2a+bЃМ0ЃЛЂлb2Љ4ac=0ЃЛЂм8a+cЃМ0ЃЛЂнaЃКbЃКc=Љ1ЃК2ЃК3ЃЌЦфжае§ШЗЕФНсТлга______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНтЯТСаЗНГЬЃК
(1)2x2Ѓ4xЃ1ЃН0(ХфЗНЗЈ)ЃЛ
(2)(xЃЋ1)2ЃН6xЃЋ6.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯACB=90ЁуЃЌAB=10ЃЌsinA=![]() ЃЌCDЮЊABБпЩЯЕФжаЯпЃЌвдЕуBЮЊдВаФЃЌrЮЊАыОЖзїЁбBЃЎШчЙћЁбBгыжаЯпCDгаЧвжЛгавЛИіЙЋЙВЕуЃЌФЧУДЁбBЕФАыОЖrЕФШЁжЕЗЖЮЇЮЊ_____ЃЎ
ЃЌCDЮЊABБпЩЯЕФжаЯпЃЌвдЕуBЮЊдВаФЃЌrЮЊАыОЖзїЁбBЃЎШчЙћЁбBгыжаЯпCDгаЧвжЛгавЛИіЙЋЙВЕуЃЌФЧУДЁбBЕФАыОЖrЕФШЁжЕЗЖЮЇЮЊ_____ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
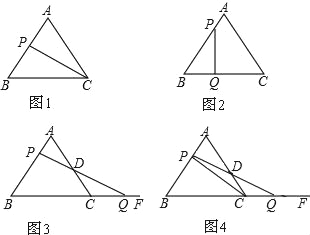
ЁОЬтФПЁПвбжЊЃЌЁїABCЪЧБпГЄ3cmЕФЕШБпШ§НЧаЮЃЎЖЏЕуPвд1cm/sЕФЫйЖШДгЕуAГіЗЂЃЌбиЯпЖЮABЯђЕуBдЫЖЏЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌЩшЕуPЕФдЫЖЏЪБМфЮЊtЃЈsЃЉЃЌФЧУДtЃНЁЁ ЁЁЃЈsЃЉЪБЃЌЁїPBCЪЧжБНЧШ§НЧаЮЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌШєСэвЛЖЏЕуQДгЕуBГіЗЂЃЌбиЯпЖЮBCЯђЕуCдЫЖЏЃЌШчЙћЖЏЕуPЁЂQЖМвд1cm/sЕФЫйЖШЭЌЪБГіЗЂЃЎЩшдЫЖЏЪБМфЮЊtЃЈsЃЉЃЌФЧУДtЮЊКЮжЕЪБЃЌЁїPBQЪЧжБНЧШ§НЧаЮЃП
ЃЈ3ЃЉШчЭМ3ЃЌШєСэвЛЖЏЕуQДгЕуCГіЗЂЃЌбиЩфЯпBCЗНЯђдЫЖЏЃЎСЌНгPQНЛACгкDЃЎШчЙћЖЏЕуPЁЂQЖМвд1cm/sЕФЫйЖШЭЌЪБГіЗЂЃЎЩшдЫЖЏЪБМфЮЊtЃЈsЃЉЃЌФЧУДtЮЊКЮжЕЪБЃЌЁїDCQЪЧЕШбќШ§НЧаЮЃП
ЃЈ4ЃЉШчЭМ4ЃЌШєСэвЛЖЏЕуQДгЕуCГіЗЂЃЌбиЩфЯпBCЗНЯђдЫЖЏЃЎСЌНгPQНЛACгкDЃЌСЌНгPCЃЎШчЙћЖЏЕуPЁЂQЖМвд1cm/sЕФЫйЖШЭЌЪБГіЗЂЃЎЧыФуВТЯыЃКдкЕуPЁЂQЕФдЫЖЏЙ§ГЬжаЃЌЁїPCDКЭЁїQCDЕФУцЛ§гаЪВУДЙиЯЕЃПВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com