
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���M������Ϊ��2��8������N������Ϊ��2��6�������߶�MN����ƽ��4����λ���ȵõ��߶�PQ����P�͵�Q�ֱ��ǵ�M�͵�N�Ķ�Ӧ�㣩������MP��NQ����K���߶�MP���е㣮
��1�����K�����ꣻ
��2����������PMNQ��ÿ��1����λ���ȵ��ٶ������·��˶�������A��B��C��D��E�ֱ��ǵ�M��N��Q��P��K�Ķ�Ӧ�㣩����BC��x���غ�ʱֹͣ�˶�������OA��OE�����˶�ʱ��Ϊt�룬���ú�t��ʽ�ӱ�ʾ������OAE�����S����Ҫ��д��t��ȡֵ��Χ����
��3���ڣ�2���������£�����OB��OD�����Ƿ����ijһʱ��t��ʹ������OBD���������������OAE������������ڣ������tֵ���������ڣ���˵�����ɣ�

���𰸡���1����4��8����2��S��OAE��8��t��3��2���6��
��������
��1������M��N�������ƽ�Ƶ����ʿ�֪��MN��y���PQ������K��PM���е�ɵ�K�����ꣻ
��2�����������������ʽ�ɵ�������OAE�����S��
��3���������������
����ͼ2������B��OD�Ϸ�ʱ
����ͼ3������B��OD�Ϸ�ʱ��
����B��BG��x����G����D��DH��x����H���ֱ����������OBD���������������OAE������з��̿ɵý��ۣ�
��1��������ã�PM��4��
��K��PM���е㣬
��MK��2��
�ߵ�M������Ϊ��2��8������N������Ϊ��2��6����
��MN��y�ᣬ
��K��4��8����
��2����ͼ1��ʾ���ӳ�DA��y����F��
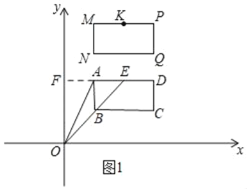
��OF��AE��F��0��8��t����
��OF��8��t��
��S��OAE��![]() OFAE��
OFAE��![]() ��8��t����2��8��t��
��8��t����2��8��t��
��3�����ڣ��������������
����ͼ2������B��OD�Ϸ�ʱ��

����B��BG��x����G����D��DH��x����H����B��2��6��t����D��6��0����
��OG��2��GH��4��BG��6��t��DH��8��t��OH��6��
S��OBD��S��OBG+S�ı���DBGH+S��ODH��
��![]() OGBG+
OGBG+![]() ��BG+DH��GH��
��BG+DH��GH��![]() OHDH��
OHDH��
��![]() ��2��6-t��+
��2��6-t��+![]() ��4��6��t+8��t����
��4��6��t+8��t����![]() ��6��8��t����
��6��8��t����
��10��2t��
��S��OBD��S��OAE��
��10��2t��8��t��
t��2��
����ͼ3������B��OD�Ϸ�ʱ��
����B��BG��x����G����D��DH��x����H��
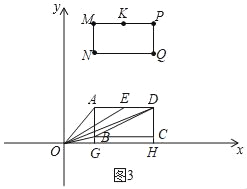
��B��2��6��t����D��6��8��t����
��OG��2��GH��4��BG��6��t��DH��8��t��OH��6��
S��OBD��S��ODH��S�ı���DBGH��S��OBG��
��![]() OHDH��
OHDH��![]() ��BG+DH��GH��
��BG+DH��GH��![]() OGBG��
OGBG��
��![]() ��2��8-t����
��2��8-t����![]() ��4��6��t+8��t����
��4��6��t+8��t����![]() ��2��6��t����
��2��6��t����
��2t��10��
��S��OBD��S��OAE��
��2t��10��8��t��
t��6��
���ϣ�t��ֵ��2���6�룮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��CEƽ�֡�BCD����1����2��70�㣬��3��40�㣬AB��CD�Ƿ�ƽ�У���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
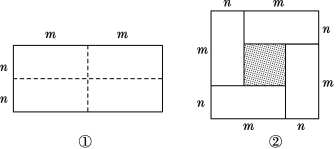
����Ŀ��ͼ����һ����Ϊ2m����Ϊ2n�ij����Σ���ͼ�������ü����������ֳ��ĸ�С�����Σ�Ȼ��ͼ�ڵ���״ƴ��һ�������Σ�
(1)����Ϊͼ���е���Ӱ���ֵ������εı߳����ڶ��٣�
(2)�������ֲ�ͬ�ķ�����ͼ������Ӱ���ֵ������
(3)�۲�ͼ������д��������������ʽ֮��ĵ�����ϵ��
����ʽ��(m��n)2��(m��n)2��mn.
(4)����(3)���еĵ�����ϵ������������⣺
��֪a��b��7��ab��5����(a��b)2��ֵ��(д������)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
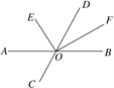
����Ŀ����ͼ��ֱ��AB��CD���ڵ�O��OEƽ�֡�AOD��OFƽ�֡�BOD.
(1)��AOC��50�������DOF���DOE�Ķ������������EOF�Ķ�����
(2)����AOC�Ķ����仯ʱ����EOF�Ķ����Ƿ�仯�������䣬����ֵ�����仯��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����E����F��90������B����C��AE��AF�������½��ۣ���EM��FN����CD��DN���ۡ�FAN����EAM���ܡ�ACN�ա�ABM��������ȷ���У� ����
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס������˽���������ϰ������·��y���ף�������ʱ��t�����ӣ�֮��Ĺ�ϵ��ͼ��ʾ������˵����������� ��

A. ǰ2���ӣ��ҵ�ƽ���ٶȱȼ�
B. 5����ʱ���˶�����500��
C. ������800��ƽ���ٶ�Ϊ100��/��
D. ��������8���Ӹ�����800��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ���x2+mx+m��2=0��
��1����֤������mȡ��ֵʱ������������������ȵ�ʵ������
��2���跽����ʵ�����ֱ�Ϊx1 �� x2 �� ������x12+x22=��3x1x2 �� ��ʵ��m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y=ax2��2ax��3a��a��0����x�ύ��A��B���㣨��A�ڵ�B��ࣩ��������A��ֱ��l��y=kx+b��y�ύ�ڵ�C���������ߵ���һ������ΪD����CD=4AC��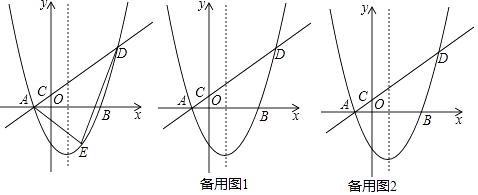
��1��ֱ��д����A�����꣬���ú�a��ʽ�ӱ�ʾֱ��l�ĺ�������ʽ������k��b�ú�a��ʽ�ӱ�ʾ����
��2����EΪֱ��l�·���������һ�㣬����ADE����������ֵΪ ![]() ʱ���������ߵĺ�������ʽ��
ʱ���������ߵĺ�������ʽ��
��3�����P�������߶Գ����ϵ�һ�㣬��Q���������ϣ��Ե�A��D��P��QΪ������ı����ܷ�Ϊ���Σ����ܣ������P�����ꣻ�����ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com