
【题目】如图所示,∠E=∠F=90°,∠B=∠C,AE=AF.有以下结论:①EM=FN;②CD=DN;③∠FAN=∠EAM;④△ACN≌△ABM.其中正确的有( ).
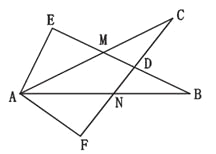
A. 1个 B. 2个 C. 3个 D. 4个
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知y与x的关系的图象如图所示,根据图象回答下列问题:
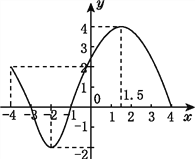
(1)确定自变量x的取值范围.
(2)当x=-4,-2,4时,y的值分别是多少?
(3)当y=0,4时,x的值分别是多少?
(4)当x取何值时,y的值最大?当x取何值时,y的值最小?
(5)当x的值在什么范围内时,y随x的增大而增大?当x的值在什么范围内时,y随x的增大而减小?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆快车从甲地开往乙地,一辆慢车从乙地开往甲地,两车同时出发,设慢车离乙地为y1(km),快车离乙地的距离为y2(km),慢车行驶时间为x(h),两车之间的距离为s(km),y1 ,y2与x的函数关系图像如图①所示,s与x的函数关系图如图②所示:

图① 图②
(1)图中的a= ,b= .
(2)求s关于x的函数关系式.
(3)甲、乙两地间有E、F两个加油站,相距200km,若慢车进入加油站E时,快车恰好进入加油站F,请直接写出加油站E到甲地的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c过点A(﹣4,﹣3),与y轴交于点B,对称轴是x=﹣3,请解答下列问题:
(1)求抛物线的解析式.
(2)若和x轴平行的直线与抛物线交于C,D两点,点C在对称轴左侧,且CD=8,求△BCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究题
(1)【证法回顾】
证明:三角形中位线定理.
已知:如图1,DE是△ABC的中位线.
求证:DE∥BC,DE= ![]() BC.
BC.
证明:添加辅助线:如图1,在△ABC中,延长DE (D、E分别是AB、AC的中点)到点F,使得EF=DE,连接CF;请继续完成证明过程: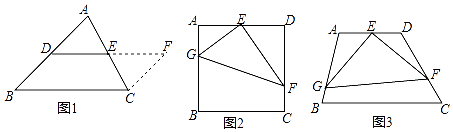
(2)【问题解决】
如图2,在正方形ABCD中,E为AD的中点,G、F分别为AB、CD边上的点,若AG=2,DF=3,∠GEF=90°,求GF的长.
(3)【拓展研究】如图3,在四边形ABCD中,∠A=105°,∠D=120°,E为AD的中点,G、F分别为AB、CD边上的点,若AG=3 ![]() ,DF=2,∠GEF=90°,求GF的长.
,DF=2,∠GEF=90°,求GF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90,AC=3,BC=4,分别以AB、AC、BC为边在AB同侧作正方形ABEF,ACPQ,BDMC,记四块阴影部分的面积分别为S1、S2、S3、S4 , 则S1+S2+S3+S4= . 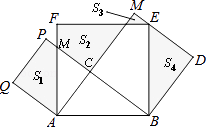
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“2014年至2016年,中国同‘一带一路’沿线国家贸易总额超过3万亿美元”,将数据3万亿美元用科学记数法表示为( )
A.3×1014美元
B.3×1013美元
C.3×1012美元
D.3×1011美元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com