
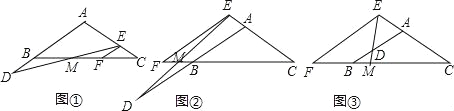
����Ŀ���ڵ���������ABCD�У�AB=AC���ֱ�������AB��CA��ȡ��D��E������DE������E��EF��AB��ֱ��BC�ڵ�F��ֱ��BC��DE����ֱ�߽��ڵ�M��
���룺��ͼ�٣���D�ڱ�AB�ӳ����ϣ���E�ڱ�AC�ϣ���BD=CE�����߶�BM��EM�Ĵ�С��ϵΪ ��
̽������ͼ�ڣ���D��E�ֱ��ڱ�AB��CA�ӳ����ϣ���BD=CE���ж��߶�DM��EM�Ĵ�С��ϵ��������֤����
��չ����ͼ�ۣ���D�ڱ�AB�ϣ���D�����A��B�غϣ�����E�ڱ�CA���ӳ����ϣ������������䣬��BD=1��CE=4��DM=0.7�����߶�DE�ij�Ϊ ��
���𰸡����룺DM=EM��̽����DM=EM����չ��2.1.
��������
�����������1�����ݵ��������ε����ʺ�ƽ���ߵ����ʵõ���D=��MEF��֤����BDM�ա�FEM���ɣ�
��2�����ݵ��������ε����ʺ�ƽ���ߵ����ʵõ���D=��MEF��֤����BDM�ա�FEM���ɣ�
��3�����ݵ��������ε����ʺ�ƽ���ߵ����ʵõ�EF=CE��BD��EF��![]() ���������ݼ��ɵõ����ۣ�
���������ݼ��ɵõ����ۣ�
�����������1�����룺DM=EM��
���ɣ���AB=AC��
���ABC=��C��
��EF��AD��
���EFC=��ABC��
���C=��EFC��
��EF=EC��
��BD=EC��
��DB=EF��
��EF��AB��
���D=��MEF��
�ڡ�BDM�͡�FEM�У�
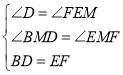 ��
��
���BDM�ա�FEM��
��DM=EM��
��2������DM=EM��
���ɣ���AB=AC��
���ABC=��C��
��EF��AB��
���EFC=��ABC��
���C=��EFC��
��EF=EC��
��BD=EC��
��DB=EF��
��EF��AB��
���D=��MEF��
�ڡ�BDM�͡�FEM�У�
 ��
��
���BDM�ա�FEM��
��DM=EM��
��3����EF��AB��
���F=��ABC��
��AB=AC��
���ABC=��C��
���F=��C��
��EF=CE=4��
��BD��EF��
��![]() ��
��
��![]() ��
��
��EM=2.8��
��DE=EM-DM=2.1��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ�٣��ھ���ABCD�У���E�DZ�BC���е㣬����ABE��AE�۵���ʹ��B���ھ���ABCD�ڲ��ĵ�F�����ӳ�AF��CD�ڵ�G������FC����֤��GCF=��GFC��
̽������ͼ���еľ���ABCD��Ϊƽ���ı��Σ������������䣬��ͼ�ڣ��жϡ�GCF=��GFC�Ƿ���Ȼ��ȣ���˵�����ɣ�
Ӧ�ã���ͼ�ڣ���AB=5��BC=6�����ADG���ܳ�Ϊ ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���С��ͬʱ��ѧУ�������Ƽ��ݲμӻ��С��ÿСʱ��6ǧ�ף�С��ÿСʱ��8ǧ�ף�����1Сʱ��С���������Ϸ���ѧУȡ���ϣ�������ԭ·ȥС�㣮С����Сʱ��С�㣿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���������εױ߳�Ϊ6cm������Ϊ5cm���������ܳ�Ϊ( ).
A.19
B.16
C.14
D.16��17
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ���ǣ�������
A. �������ĺ�Ϊ�㣬�����ǻ�Ϊ�෴�� B. �����ĵ���һ����ԭ����
C. �����෴���ǣ�3.14 D. ԭ��һ���������෴��С
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y=����x+2��2��3����ƽ����3����λ����ôƽ�ƺ������ߵĶ��������ǣ�������
A. ����5����3�� B. ����2��0�� C. ����1����3�� D. ��1����3��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com