
| 1 |
| 1×2 |
| 1 |
| 2 |
| 1 |
| 2×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3×4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 9×10 |
| 1 |
| 9 |
| 1 |
| 10 |
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 9×10 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 9 |
| 1 |
| 10 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 9 |
| 1 |
| 10 |
| 1 |
| 10 |
| 9 |
| 10 |
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 2004×2005 |
| 1 |
| 2005×2006 |
| 1 |
| 1×3 |
| 1 |
| 3×5 |
| 1 |
| 5×7 |
| 1 |
| 49×51 |
| 1 |
| n×(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n×(2n-1) |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| 2n-1 |
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 2004×2005 |
| 1 |
| 2005×2006 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2005 |
| 1 |
| 2006 |
| 1 |
| 2006 |
| 2005 |
| 2006 |
| 1 |
| 1×3 |
| 1 |
| 3×5 |
| 1 |
| 5×7 |
| 1 |
| 49×51 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 49 |
| 1 |
| 51 |
| 1 |
| 2 |
| 1 |
| 51 |
| 1 |
| 2 |
| 50 |
| 51 |
| 25 |
| 51 |


 优生乐园系列答案
优生乐园系列答案科目:初中数学 来源: 题型:
 (阅读理解题)如图所示,CE⊥AB于点E,BD⊥AC于点D,BD,CE交于点O,且AO平分∠BAC.
(阅读理解题)如图所示,CE⊥AB于点E,BD⊥AC于点D,BD,CE交于点O,且AO平分∠BAC.查看答案和解析>>
科目:初中数学 来源:2012届重庆奉节县直中学八年级下学期期中考试数学卷(带解析) 题型:解答题
阅读理解:对于二次三项式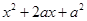 可以直接用公式法分解为
可以直接用公式法分解为 的形式,但对于二次三项式
的形式,但对于二次三项式 ,就不能直接用公式法了,我们可以在二次三项式
,就不能直接用公式法了,我们可以在二次三项式 中先加上一项
中先加上一项 ,使其成为完全平方式,再减去
,使其成为完全平方式,再减去 这项,使整个式子的值不变.于是有
这项,使整个式子的值不变.于是有 =
= +
+ -
-
= =
= =
= 。
。
像上面这样把二次三项式分解因式的方法叫做添(拆)项法.
【小题1】请用上述方法求出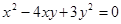 (满足
(满足 ,且
,且 )中
)中 与
与 的关系式。
的关系式。
【小题2】利用上述关系式求 的值。
的值。
查看答案和解析>>
科目:初中数学 来源:2012-2013学年浙江宁波青山中学九年级下学期第一次月考数学试卷(解析版) 题型:解答题
阅读题
先阅读理解,再回答下列问题:
因为 ,且
,且 ,所以
,所以 的整数部分为1;
的整数部分为1;
因为 ,且
,且 ,所以
,所以 的整数部分为2;
的整数部分为2;
因为 ,且
,且 ,所以
,所以 的整数部分为3;
的整数部分为3;
以此类推,我们会发现 为正整数)的整数部分为______,请说明理由.
为正整数)的整数部分为______,请说明理由.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 1 |
| 1×2 |
| 1 |
| 2 |
| 1 |
| 2×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3×4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 9×10 |
| 1 |
| 9 |
| 1 |
| 10 |
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 9×10 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 9 |
| 1 |
| 10 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 9 |
| 1 |
| 10 |
| 1 |
| 10 |
| 9 |
| 10 |
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 2004×2005 |
| 1 |
| 2005×2006 |
| 1 |
| 1×3 |
| 1 |
| 3×5 |
| 1 |
| 5×7 |
| 1 |
| 49×51 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com