
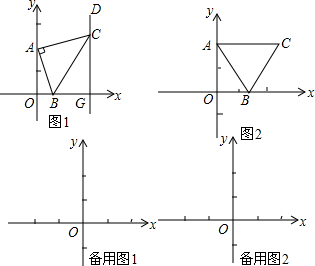
ñøö— È´1Èˋ¿»Cæ¼CMÀëyøÃȘÀ¼DMAÀíÀ¼AOBȘ¢èúµçûDMçá°ÊȘ¢èçû°—DEçáÝÚÇÿò§È£
È´2ÈˋÂì¿»Cæ¼CNÀëxøÃÆÖçÐNȘÆèçàÝÔ໧úÅöçáÅåøò¢èúµçûCN¤ëONȘ¢èúµçûCçÐæ½ÝõÈ£ÂÖ¢èåìúµçûôºæÐä¾¥±çáØ£¡—CçÐȘàÓçÝCÈ´0Ș-2ÈˋòÝȘôºæÐä¾¥±È˜â«ÆûǻѴüçò»ò»ñ´¢èúµçûøÝüÔÝÚÇÿò§È£ÂÜØåCöˆåýÅáȘCE°Êöˆ¯ŠƒÑ£ÙåýȘçÝ¡ûåý¿»çÐOòÝȘÇùòÝCEÆÅæŸÇµøçÈ´àÀý£ç§¡ûøçÈˋȘçÝ¡ûåýÆŠyøÃüÁúÅòÝȘCEÆÅæŸÅÀøçȘå졪ƒïçàî■໧úÅö¤ëó§ÅÅüÔñøüÔÑö°èÝàâ»ñøÝÞúµçûCEçáøçȘ¥Ç¢èúµçûÇÞ¯¡ÈÛ
§ãÇÞ §ãȤ
È´1Èˋ¿»Cæ¼CMÀëyøÃÆÖçÐMȘàÓë¥1Ș
ÀÔÀüBAC=90ÀÐȘ
ÀÁÀüCAM+ÀüBAO=ÀüMCA+ÀüCAM=90ÀÐȘ
ÀÁÀüBAO=ÀüMCAȘ
åÖÀ¼DMA¤ëÀ¼AOBøÅ
$\left\{\begin{array}{l}{ÀüMCA=ÀüBAO}\\{ÀüCMA=ÀüAOB}\\{AC=AB}\end{array}\right.$
ÀÁÀ¼DMAÀíÀ¼AOBÈ´AASÈˋȘ
ÀÁMC=OA=2ȘúØDEÀëxøÃȘ
ÀÁøÝüÔDEçáÝÚÇÿò§öˆx=2Ș
¿òÇÞ¯¡öˆÈ¤x=2È£
È´2ÈˋÂì¿»Cæ¼CNÀëxøÃÆÖçÐNȘàÓë¥2Ș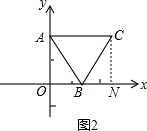
ÀÔACÀöxøÃȘ
ÀÁCN=AO=2Ș
ÆøÀ¼ABCöˆçàÝÔ໧úÅöȘ
ÀÁÀüACB=60ÀÐȘ
ÀÁÀüBCN=30ÀÐȘ
ÀÁAC=BC=$\frac{CN}{cos30ÀÐ}$=$\frac{4\sqrt{3}}{3}$Ș
ÀÁCçÐæ½ÝõöˆÈ´$\frac{4\sqrt{3}}{3}$Ș2ÈˋȘ
¿òÇÞ¯¡öˆÈ¤È´$\frac{4\sqrt{3}}{3}$Ș2ÈˋÈ£
ÂÖÆèÂìøˆCçÐæ½ÝõöˆÈ´$\frac{4\sqrt{3}}{3}$Ș2ÈˋȘ
úØçÝCÈ´0Ș-2ÈˋòÝȘÆèAÀÂC¿ÄÆÖxøÃÑå°ó¢èøˆåÖxøÃèüÇÌåÖBçÐò¿À¼ABCöˆçàÝÔ໧úÅöȘ
ÀÁçÐÈ´0Ș-2ÈˋØýåÖCçÐùªÅö°èçáøÝüÔèüȘ
èÒøÝüÔÝÚÇÿò§öˆy=kx+bȘ
¯îçÐÈ´$\frac{4\sqrt{3}}{3}$Ș2Èˋ¤ëÈ´0Ș-2ÈˋÇºàŠ¢èçû$\left\{\begin{array}{l}{-2=b}\\{2=\frac{4\sqrt{3}}{3}k+b}\end{array}\right.$Ș§ãçû$\left\{\begin{array}{l}b=-2\\ k=\sqrt{3}\end{array}\right.$ÈÛ
ÀÁøÝüÔçáÝÚÇÿò§òúy=$\sqrt{3}$x-2È£
Ñ₤çÐCåùÑ₤Åö°èøÝüÔàÓë¥3ùªòƒ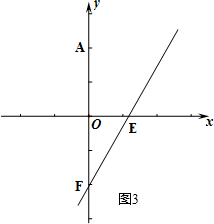
ÂÜçÝçÐCåÖüÔÑöEFèüòÝȘØåCöˆåýÅáȘCE°Êöˆ¯ŠƒÑ£ÙåýȘ
çÝåý¿»çÐOòÝȘàÓë¥4ȘÝÔ§ÆCOȘ¢èøˆÇùòÝCE柰ÊȘ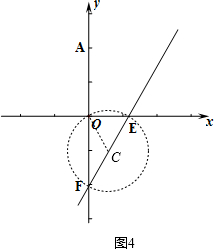
ÆèÂÖ¢èúµçûEçÐæ½ÝõöˆÈ´$\frac{2\sqrt{3}}{3}$Ș0ÈˋȘFÈ´0Ș-2ÈˋȘ
Æè¿Ç¿èÑ´âÚ¢èúµçûEF=$\frac{4\sqrt{3}}{3}$Ș
ÆèåýøɧúÑ´âÚ¢èøˆÇùòÝCE=$\frac{1}{2}$EF=$\frac{2\sqrt{3}}{2}$Ș
çÝåýÆŠyøÃüÁúÅòÝȘå·úÅçÐ¥ÇöˆôºæÐä¾¥±çáçÐHȘ꘧ÆCHȘàÓë¥5Ș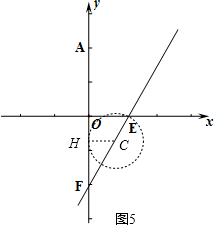
ÇùòÝCEçáøçòÝÅÀȘ
ÀÔHCÀöOEȘúØCH=CEȘ
ÀÁ$\frac{HC}{OE}$=$\frac{FC}{EF}$=$\frac{EF-CE}{EF}$=$\frac{CE}{OE}$Ș¥Ç$\frac{\frac{4\sqrt{3}}{3}-CE}{\frac{4\sqrt{3}}{3}}$=$\frac{CE}{\frac{2\sqrt{3}}{3}}$Ș§ãçûCE=$\frac{4\sqrt{3}}{9}$Ș
ÆøçÐHÆŠOÀÂFý£øĤüȘ
ÀÁCEàÀý£ç§æŸÇµøçȘ
ÀÁCEçáàÀøçñÑöÏöˆ$\frac{4\sqrt{3}}{9}$ÀÉCEÈ¥$\frac{2\sqrt{3}}{3}$Ș
¿òÇÞ¯¡öˆÈ¤$\frac{4\sqrt{3}}{9}$ÀÉCEÈ¥$\frac{2\sqrt{3}}{3}$ÈÛ
çÐóâ ݃äãø¼Øˆ¢¥ýÕØ£Çö¤₤ò»çáæܤüÆÎÆûȘèÌ¥¯øˆòÑçÐÆÅà¨çà໧úÅöçáéÅÑ´¤ëÅåøòÀÂǻѴüçò»ñ´ÀÂçàÝÔ໧úÅöçáÅåøòÀÂåýçáÆÅ¿ÄÅåøòçàÈÛåÖÈ´1ÈˋøÅúµçûCç§yøÃçáƒÁâŠòú§ãäãçá¿Ä¥■ȘåÖÈ´2ÈˋÂÜøÅàñÑ´°—CEçáæŸÇµøç¤ëæŸÅÀøçòú§ãäãçá¿Ä¥■ÈÛ݃äãøˆòÑçЧüÑÁȘæܤüÅå§üú¢È˜ç¨áîÑàý£ÇµÈÛ


 äšäšü·èüأ݃¤ûƒÚüçêÅÇÞ¯¡
äšäšü·èüأ݃¤ûƒÚüçêÅÇÞ¯¡ ÅÀîÏèº10ñøøÆÆÎÆûäãüçêÅÇÞ¯¡
ÅÀîÏèº10ñøøÆÆÎÆûäãüçêÅÇÞ¯¡
| áõ¥Ñ | ¡ÔøÅ¢ö°ä | áõ¥Ñ | °¾øÅ¢ö°ä |
| ¡ÔØ£ | ¡ÔØ£ûãñî¢ö°äëó¥—ÈÀ | °¾Ø£ | °¾Ø£ûãñî¢ö°äëó¥—ÈÀ |
| ¡Ôѱ | ¡Ôѱûãñî¢ö°äëó¥—ÈÀ | °¾Ñ± | °¾Ñ±ûãñî¢ö°äëó¥—ÈÀ |
| ¡Ôà» | ¡Ôà»ûãñî¢ö°äëó¥—ÈÀ | °¾à» | °¾à»ûãñî¢ö°äëó¥—ÈÀ |
¢óá¢È¤°¾øÅò»îÏ âÇåÇȤ äãÅëȤ䟢íäã
ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤°¾øÅò»îÏ âÇåÇȤ äãÅëȤ§ãÇÞäã
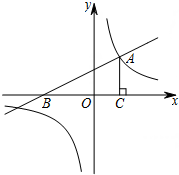 àÓë¥È˜Ø£Çö¤₤ò»y=$\frac{1}{2}$x+2çáë¥üµÆŠxøç£ÆÖçÐBȘƊñÇÝà⻤₤ò»y=$\frac{k}{x}$çáë¥üµçáØ£¡—§£çÐöˆAÈ´2ȘmÈˋÈÛ
àÓë¥È˜Ø£Çö¤₤ò»y=$\frac{1}{2}$x+2çáë¥üµÆŠxøç£ÆÖçÐBȘƊñÇÝà⻤₤ò»y=$\frac{k}{x}$çáë¥üµçáØ£¡—§£çÐöˆAÈ´2ȘmÈˋÈÛýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤°¾øÅò»îÏ âÇåÇȤ äãÅëȤ䟢íäã
ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤°¾øÅò»îÏ âÇåÇȤ äãÅëȤ§ãÇÞäã
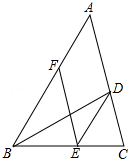 àÓë¥È˜BDòúÀ¼ABCçá§úó§ñøüÔȘçÐEȘFñøÝÞåÖBCȘABèüȘúØDEÀöABȘBE=AFÈÛ
àÓë¥È˜BDòúÀ¼ABCçá§úó§ñøüÔȘçÐEȘFñøÝÞåÖBCȘABèüȘúØDEÀöABȘBE=AFÈÛýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤°¾øÅò»îÏ âÇåÇȤ äãÅëȤîÀåþäã
| °è¥´È´ÇöÈˋ | 43 | 45 | 46 | 47 | 48 | 49 | 51 |
| àùò» | 2 | 3 | 5 | 7 | 4 | 2 | 2 |
| AÈÛ | 47Ș46 | BÈÛ | 47Ș47 | CÈÛ | 45Ș48 | DÈÛ | 51Ș47 |
ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤°¾øÅò»îÏ âÇåÇȤ äãÅëȤ§ãÇÞäã
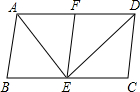 àÓë¥È˜Øîøˆó§ÅÅùáÝÔÅöABCDȘîÄæéDEíÜ籤µçÐCôðåÖADÝÔèüçáFÇÎÈÛ
àÓë¥È˜Øîøˆó§ÅÅùáÝÔÅöABCDȘîÄæéDEíÜ籤µçÐCôðåÖADÝÔèüçáFÇÎÈÛýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤°¾øÅò»îÏ âÇåÇȤ äãÅëȤ§ãÇÞäã
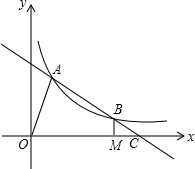 àÓë¥È˜øÝüÔAB§£ù¨úºüÔy=$\frac{k}{x}$È´xȃ0ÈˋÆÖAÀÂBê§çÐȘ§£xøÃÆÖçÐCÈ´4aȘ0ÈˋȘAB=2BCȘ¿»çÐBæ¼BMÀëxøÃÆÖçÐMȘ꘧ÆOAȘà¶OM=3MCȘSÀ¼OAC=8ȘúµkçáøçÈÛ
àÓë¥È˜øÝüÔAB§£ù¨úºüÔy=$\frac{k}{x}$È´xȃ0ÈˋÆÖAÀÂBê§çÐȘ§£xøÃÆÖçÐCÈ´4aȘ0ÈˋȘAB=2BCȘ¿»çÐBæ¼BMÀëxøÃÆÖçÐMȘ꘧ÆOAȘà¶OM=3MCȘSÀ¼OAC=8ȘúµkçáøçÈÛýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¿º¥òîÏÅÈÆéîÀ - êñü¯ýÃêÅÝÚ - òåäãêÅÝÚ
¤±ÝÝòÀ£Ëêˆë½öËñ´¤ëý£ê¥ÅéüƒìÝ´ó§ä´ | ë½èüÆŤÎÅéüƒìÝ´æ´ú½ | çÓÅéíˋóÙƒìÝ´æ´ú½ | èÌâºòñÅÕößø¼ØÍÆŤÎÅéüƒìÝ´æ´ú½ | èÌóµúøà´ƒìÝ´æ´ú½
öËñ´¤ëý£ê¥ÅéüƒìÝ´çÓ£¯È¤027-86699610 ƒìÝ´ÆòüðȤ58377363@163.com