
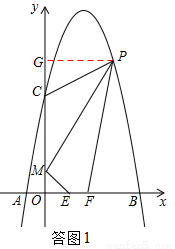
如图,对称轴为直线x=2的抛物线经过点A(-1,0),C(0,5)两点,与x轴另一交点为B,已知M(0,1),E(a,0),F(a+1,0),点P是第一象限内的抛物线上的动点.
(1)求此抛物线的解析式;
(2)当a=1时,求四边形MEFP面积的最大值,并求此时点P的坐标;
(3)若△PCM是以点P为顶点的等腰三角形,求a为何值时,四边形PMEF周长最小?请说明理由.

(1)y=-x2+4x+5;(2)当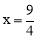 时,四边形MEFP面积的最大,最大值为
时,四边形MEFP面积的最大,最大值为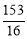 ,此时点P坐标为
,此时点P坐标为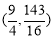 ;(3)当
;(3)当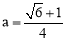 时,四边形FMEF周长最小.
时,四边形FMEF周长最小.
【解析】
试题分析:(1)设顶点式,利用待定系数法求出抛物线的解析式.
(2)求出四边形MEFP面积的表达式,利用二次函数的性质求出最值及点P坐标.
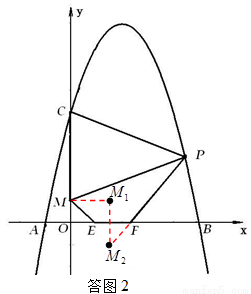
(3)四边形PMEF的四条边中,PM、EF长度固定,因此只要ME+PF最小,则PMEF的周长将取得最小值.如答图2所示,将点M向右平移1个单位长度(EF的长度),得M1(1,1);作点M1关于x轴的对称点M2,则M2(1,﹣1);连接PM2,与x轴交于F点,此时ME+PF=PM2最小.
试题解析:【解析】
(1)∵抛物线的对称轴为直线x=2,∴设抛物线为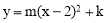 .
.
∵抛物线过点A(-1,0)、C(0,5),
∴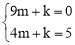 ,解得:
,解得: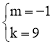 .
.
∴二次函数的函数关系式为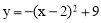 ,即y=-x2+4x+5.
,即y=-x2+4x+5.
(2)当a=1时,E(1,0),F(2,0),
设P的坐标为(x,-x2+4x+5)
如答图1,过点P作y轴的垂线,垂足为G,
则四边形MEFP面积
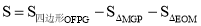 =
=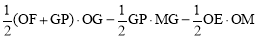
=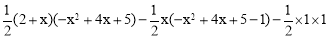 =
=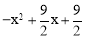 =
=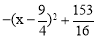 ,
,
∴当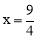 时,四边形MEFP面积的最大,最大值为
时,四边形MEFP面积的最大,最大值为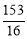 ,此时点P坐标为
,此时点P坐标为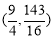 .
.
(3)如答图2,把点M向右平移1个单位得点M1,再做点M1关于x轴的对称点M2,在四边形FMEF中,因为边PM,EF为固定值,所以要使四边形FMEF周长最小,则ME+PF最小,因为ME=M1F=M2F,所以只要使M2F+PF最小即可,所以点F应该是直线M2P与x轴的交点,由OM=1,OC=5,得点P的纵坐标为3,根据y=-x2+4x+5可求得点P(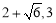 )
)
又点M2坐标为(1,-1),∴直线M2P的解析式为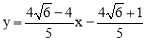 .
.
当y=0时,求得 ,∴F(
,∴F(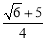 ,0).∴
,0).∴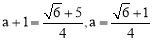 .
.


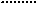 ∴当
∴当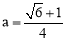 时,四边形FMEF周长最小.
时,四边形FMEF周长最小.
考点:1. 二次函数综合题;2.单动点问题;3.待定系数法的应用;4.曲线上点的坐标与方程的关系;5.二次函数的性质;6.由实际问题列函数关系式;7.等腰三角形的性质;8.轴对称的应用(最短线路问题).


科目:初中数学 来源:2014年初中毕业升学考试(浙江绍兴卷)数学(解析版) 题型:填空题
如图,边长为n的正方形OABC的边OA,OC在坐标轴上,点A1,A2…An﹣1为OA的n等分点,点B1,B2…Bn﹣1为CB的n等分点,连结A1B1,A2B2,…An﹣1Bn﹣1,分别交曲线 (x>0)于点C1,C2,…,Cn﹣1.若C15B15=16C15A15,则n的值为 .(n为正整数)
(x>0)于点C1,C2,…,Cn﹣1.若C15B15=16C15A15,则n的值为 .(n为正整数)

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(海南卷)数学(解析版) 题型:选择题
一个圆锥的侧面展开图是半径为8cm、圆心角为120°的扇形,则此圆锥底面圆的半径为( )
A. cm B.
cm B.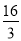 cm C.
cm C. cm D.
cm D. cm
cm
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(海南卷)数学(解析版) 题型:解答题
海南有丰富的旅游产品.某校九年级(1)班的同学就部分旅游产品的喜爱情况对游客随机调查,要求游客在列举的旅游产品中选出喜爱的产品,且只能选一项,以下是同学们整理的不完整的统计图:
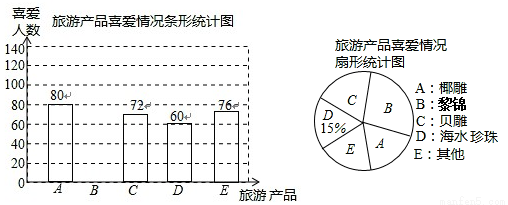
根据以上信息完成下列问题:
(1)请将条形统计图补充完整;
(2)随机调查的游客有 人;在扇形统计图中,A部分所占的圆心角是 度;
(3)请根据调查结果估计在1500名游客中喜爱黎锦的约有 人.
查看答案和解析>>
科目:初中数学 来源:2014年沪教版初中数学七年级上册第九章9.3整式的乘法练习卷(解析版) 题型:选择题
下列各式成立的是( )
A.(a3)x=(ax)3 B.(an)3=an+3 C.(a+b)3=a2+b2 D.(﹣a)m=﹣am
查看答案和解析>>
科目:初中数学 来源:2014年沪教版初中数学七年级上册第九章9.3整式的乘法练习卷(解析版) 题型:选择题
a14不等于下列各式中的( )
A.a7•a7 B.a3•a5•a6 C.(a7)7 D.2a14﹣a14
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com