
如图,AB为⊙O的直径,直线 与⊙O相切于点C,过点A作AD⊥
与⊙O相切于点C,过点A作AD⊥ 于点D,交⊙O于点E.
于点D,交⊙O于点E.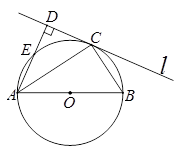
(1)求证:∠CAD=∠BAC;[(2)若sin∠BAC=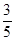 ,BC=6,求DE的长.
,BC=6,求DE的长.
(1)见解析 (2)DE=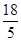
解析试题分析:(1)连接OC,根据切线性质得到AD∥CD,则∠CAD=∠ACO,根据OC=OA得到∠ACO=∠OAC,从而说明∠CAD=∠BAC;(2)做BF⊥l,连接BE,根据直径所对的圆周角等于90°说明四边形DEBF为矩形,根据垂直的定义说明∠BCF=∠BAC,根据∠BAC的正弦值得出BF的长度,从而得出DE的长度.
试题解析:(1)证明:连接OC,∵CD为⊙O的切线,∴OC⊥CD, 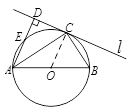
∵AD⊥CD,∴OC∥AD,∴∠CAD=∠ACO.又∵OC=OA,
∴∠ACO=∠OAC,∴∠CAD=∠OAC,即∠CAD=∠BAC.
(2)过点B作BF⊥ 于点F,连接BE,∵AB为⊙O的直径,∴∠AEB=90°,
于点F,连接BE,∵AB为⊙O的直径,∴∠AEB=90°,
又AD⊥ 于点D,∴∠AEB=∠ADF=∠BFD=90°,∴四边形DEBF是矩形,
于点D,∴∠AEB=∠ADF=∠BFD=90°,∴四边形DEBF是矩形,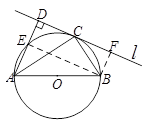
∴DE=BF. ∵AB为⊙O的直径,∴∠ACB=90°,
∴∠ACD+∠BCF=90°.∵∠ADC=90°,∴∠ACD+∠CAD=90°,
∴∠BCF=∠CAD. ∵∠CAD=∠BAC, ∴∠BCF=∠BAC.
在Rt△BCF中,BC=6, sin∠BCF=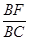 =sin∠BAC=
=sin∠BAC=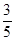 ,
,
∴BF=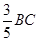 =
=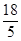 ∴DE=BF=
∴DE=BF=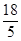 .
.
考点:切线的性质、平行线的性质、矩形的性质、锐角三角函数的应用.


科目:初中数学 来源: 题型:单选题
已知⊙O1的半径R为7cm,⊙O2的半径 为4cm,两圆的圆心距O1O2为3cm,则这两圆的位置关系是( )
为4cm,两圆的圆心距O1O2为3cm,则这两圆的位置关系是( )
| A.相交 | B.内含 | C.内切 | D.外切 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知:△OBC内接于圆,圆与直角坐标系的x、y轴交于B、A两点,若∠BOC=45°,∠OBC=75°,A点坐标为(0, ).
). 
求:⑴B点的坐标;
⑵BC的长.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省九年级上学期期中调研考试数学试卷(解析版) 题型:填空题
(本题满分6分)在一只不透明的布袋中装有红球、黄球各若干个,这些球除颜色外都相同,均匀摇匀.
(1)若布袋中有3个红球,1个黄球.从布袋中一次摸出1个球,则摸到红球的概率为 ;
(2)若布袋中有3个红球,x个黄球.请写出一个x的值 ,使得事件“从布袋中一次摸出4个球,都是黄球”是不可能的事件;
(3)若布袋中有3个红球,4个黄球.现从袋中摸出若干个球,请你设计一个必然事件: .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省九年级上学期期中考试数学试卷(解析版) 题型:选择题
已知方程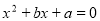 有一个根是
有一个根是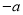 (
(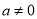 ),则下列代数式的值恒为常数的是( ).
),则下列代数式的值恒为常数的是( ).
A.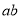 B.
B.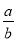 C.
C.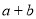 D.
D.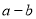
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com