
已知:△OBC内接于圆,圆与直角坐标系的x、y轴交于B、A两点,若∠BOC=45°,∠OBC=75°,A点坐标为(0, ).
). 
求:⑴B点的坐标;
⑵BC的长.
解:(1)连接AB 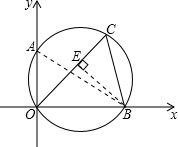
∵∠BOC=45°,∠OBC=75°,
∴∠OAB=∠OCB=60°
∵A点坐标为(0,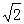 ),
),
∴AO=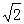 .
.
在Rt△AOB中,∠OBA=30°∴AB=2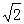
∴OB2=AB2-OA2=8-2=6
∴OB=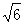
∴B(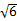 ,0)
,0)
(2)作BE⊥OC于E(4分).
∵∠BOE=45°,
∴OE=BE.
在Rt△BEO中,OE2+BE2=OB2,0E=BE=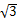
在Rt△BEC中, CE2+BE2=CB2 BC=2CE
∴BC=2
解析试题分析:(1)构造以AB为斜边的直角三角形,利用三角形的内角和定理可得∠C的度数,利用
同弧所对的圆周角相等可得∠OAB的度数,进而利用∠OAB的正切值可求得OB长,也就求得了点
B的坐标;(2)作出以BC为斜边的直角三角形,利用45°的余弦值可求得BE长,进而利用60°
的正弦值可求得BC长.
考点:解直角三角形,圆周角定理
点评:考查锐角三角函数的运用;注意构造所求边所在的有特殊角的直角三角形.


科目:初中数学 来源: 题型:解答题
如图,AB为⊙O的直径,直线 与⊙O相切于点C,过点A作AD⊥
与⊙O相切于点C,过点A作AD⊥ 于点D,交⊙O于点E.
于点D,交⊙O于点E.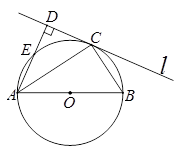
(1)求证:∠CAD=∠BAC;[(2)若sin∠BAC=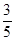 ,BC=6,求DE的长.
,BC=6,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,AC是⊙o的直径,PA切⊙o于点A,点B是⊙o上的-点,且∠BAC=30°,∠APB=60°。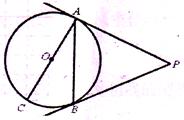
(1)求证:PB是⊙o的切线;
(2)若⊙o的半径为2,求弦AB及PA、PB的长。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省九年级上学期期中考试数学试卷(解析版) 题型:选择题
在平面直角坐标系中,抛物线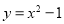 与x轴的交点个数是( )
与x轴的交点个数是( )
A.3 B.2 C.1 D.0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com