
����Ŀ��ijƷ�Ʒ�װ��˾�����г����ˣ��õ�ij���˶����������� y(��)���ۼ� x(Ԫ/��)��һ�κ��������ۼۡ��������������������� w(Ԫ)�������Ӧֵ���±���
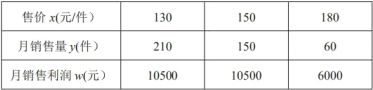
ע����������������������(�ۼ�һ����)
��1���� y ���� x �ĺ�������ʽ(��Ҫ��д���Ա�����ȡֵ��Χ)��
��2�����ۼ��Ƕ���ʱ�����������������������Ƕ���Ԫ��
��3��Ϊ��Ӧ���٣��ù�˾����ÿ�۳� 1 ����װ���;��� a Ԫ(a 0)���̼ҹ涨�÷�װ�ۼ۲��ó���200 Ԫ�����������������Ϲ�ϵ������ʱ��������������Կɴ� 9600 Ԫ���� a ��ֵ��
���𰸡���1��y=-3x��600����2�����ۼ���140Ԫʱ������������������������10800Ԫ����3��a ��ֵΪ![]()
��������
��1����y=kx��b������130,210���ͣ�150,150�����뼴��������ۣ�
��2���������˶����Ľ���ΪmԪ/������������ɵ�w=y��x��m������x=130��y=210��w=10500���뼴�����m��ֵ���Ӷ����w��x�Ķ��κ�����ϵʽ��������ö��κ�������ֵ���ɣ�
��3���������֪��w=��-3x��600����x��80��a��=-3��x��![]() ��2��
��2��![]() ��x��200����Ȼ����ݶԳ�����x��ȡֵ��Χ�������ۣ��ֱ���ݶ��κ�������������x�����Ӧ����ֵ�����ɵó����ۣ�
��x��200����Ȼ����ݶԳ�����x��ȡֵ��Χ�������ۣ��ֱ���ݶ��κ�������������x�����Ӧ����ֵ�����ɵó����ۣ�
�⣺��1�����������y=kx��b
����130,210���ͣ�150,150�����룬��
![]()
��ã�![]()
��y ���� x �ĺ�������ʽΪy=-3x��600
��2���������˶����Ľ���ΪmԪ/��
�������֪��w=y��x��m��
��x=130��y=210��w=10500���룬��
10500=210��130��m��
��ã�m=80
��w=y��x��80��=��-3x��600����x��80��=-3x2��840x��48000=-3��x��140��2��10800
��-3��0
�൱x=140ʱ��w�����ֵ�����ֵΪ10800
�𣺵��ۼ���140Ԫʱ������������������������10800Ԫ��
��3���������֪��w=��-3x��600����x��80��a��=-3��x��![]() ��2��
��2��![]() ��x��200��
��x��200��
��![]() ��200ʱ����-3��0
��200ʱ����-3��0
�൱x��200ʱ��w��x�����������
�൱x=200ʱ��w���ʱw=0���ʲ��������⣻
��![]() ��200����a��120����-3��0
��200����a��120����-3��0
��x=![]() ��w�����ֵ����ʱw�����ֵΪ
��w�����ֵ����ʱw�����ֵΪ![]()
��![]()
��ã�![]() ��������ǰ������������ȥ��
��������ǰ������������ȥ��
��![]()
��a ��ֵΪ![]() ��
��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
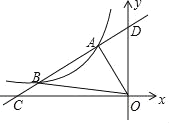
����Ŀ����ͼ��ֱ��y��kx+b�뷴��������![]() ��ͼ��ֱ��ڵ�A����1��2������B����4��n������x�ᣬy��ֱ��ڵ�C��D��
��ͼ��ֱ��ڵ�A����1��2������B����4��n������x�ᣬy��ֱ��ڵ�C��D��
��1�����һ�κ����ͷ����������Ľ���ʽ��
��2������AOB�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ָ�굽У�������п������ƶȸĸ��һ����Ҫ��ʩ��ij������ѧ�Ը�У������ָ�굽У����������������ͳ�ƣ��Ƴ�������������������ͳ��ͼ��
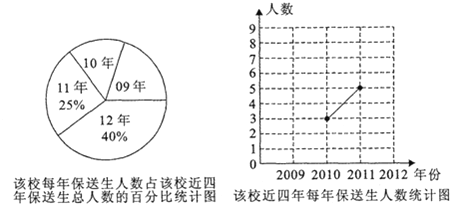
��1����У�����걣���������ļ����� ���뽫����ͳ��ͼ����������
��2����У2009��ָ�굽У��������ֻ��1λŮͬѧ��ѧУ����������ѡ��2λͬѧ�˽����ǽ��˸��нε�ѧϰ����������б�������״ͼ�ķ����������ѡ��λͬѧǡ����1λ��ͬѧ��1λŮͬѧ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һö���ػ���Ӿ��״�վC��5km�ĵ���O�����䣬����������A��Bʱ�����״�վC����õ�A��B�����Ƿֱ�Ϊ34�㣬45�������е�O��A��B��ͬһ��ֱ���ϣ���A��B�����ľ��루�����ȷ��0.1km����
���ο����ݣ�sin34��=0.56��cos34��=0.83��tan34��=0.67����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ 7x ![]() (k 13)x k 2 0 ( k ��ʵ��)������ʵ���� a��b ���� 0 a 1 b 2 ����ô k ��ȡֵ��Χ��_____��
(k 13)x k 2 0 ( k ��ʵ��)������ʵ���� a��b ���� 0 a 1 b 2 ����ô k ��ȡֵ��Χ��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
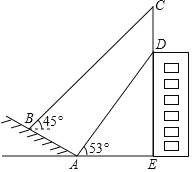
����Ŀ����ͼ��ij��¥�Ķ�������һ������CD��С����ͬѧ����ɽ�µ��½�A����ù���Ƶײ�D������Ϊ53�㣬������AB�����ߵ�B����ù���ƶ���C������Ϊ45�㣬��֪ɽ��AB���¶�![]() ��AB=10�ף�AE=21�ף�������CD�ĸ߶ȣ���������ĸ߶Ⱥ��Բ��ƣ��ο����ݣ�tan53���
��AB=10�ף�AE=21�ף�������CD�ĸ߶ȣ���������ĸ߶Ⱥ��Բ��ƣ��ο����ݣ�tan53���![]() ��cos53���0.60��
��cos53���0.60��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������Ĵ�����װ�г���ɫ���������ͬ��4��С�����к���3������Ϊ![]() ��
��![]() ��
��![]() ��������1������Ϊ
��������1������Ϊ![]() ����
����
��1�����ȴӴ���ȡ��![]() �������ٴӴ������������1��������������Ϊ�¼�
�������ٴӴ������������1��������������Ϊ�¼�![]() ����գ�����
����գ�����![]() Ϊ��Ȼ�¼�����
Ϊ��Ȼ�¼�����![]() ��ֵΪ__________������
��ֵΪ__________������![]() Ϊ����¼�����
Ϊ����¼�����![]() ��ȡֵΪ_____________��
��ȡֵΪ_____________��
��2�����Ӵ����������2�������ú������1��������״ͼ���б���������¼��ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=ax2+2ax+3a2+3������x���Ա���������x��2ʱ��y��x�������������-2��x��1ʱ��y�����ֵΪ9����a��ֵΪ![]() ����
����![]()
A. 1��![]() B. -
B. -![]() ��
��![]() C.
C. ![]() D. 1
D. 1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��һ���������칤�̣��ɼס��������̶Ӻ���20�����ɣ���������ɴ���̣����̶������������ҹ��̶ӵ�2����
��1���ס��������̶ӵ�����ɴ���̸���Ҫ�����죿
��2�����̶ӵ�����a������ɼס��������̶Ӻ����� ���죨�ú�a�Ĵ���ʽ��ʾ������ɴ���̣���֪���̶�ʩ����ÿ��1��Ԫ���ҹ��̶�ÿ��ʩ����2.5��Ԫ������̶�Ҫ����ʩ������������ɼס��������̶Ӻ������ʣ�µĹ��̣�����ʹ���̷Ѳ�����64��Ԫ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com