
 ШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌХзЮяЯпy=
ШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌХзЮяЯпy= ЃЈx-mЃЉ2-
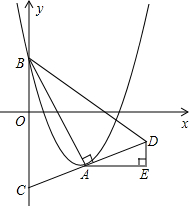
ЃЈx-mЃЉ2- m2+mЕФЖЅЕуЮЊAЃЌгыyжсЕФНЛЕуЮЊBЃЌСЌНсABЃЌACЁЭABЃЌНЛyжсгкЕуCЃЌбгГЄCAЕНЕуDЃЌЪЙAD=ACЃЌСЌНсBDЃЎзїAEЁЮxжсЃЌDEЁЮyжсЃЎ
m2+mЕФЖЅЕуЮЊAЃЌгыyжсЕФНЛЕуЮЊBЃЌСЌНсABЃЌACЁЭABЃЌНЛyжсгкЕуCЃЌбгГЄCAЕНЕуDЃЌЪЙAD=ACЃЌСЌНсBDЃЎзїAEЁЮxжсЃЌDEЁЮyжсЃЎ ЃЈx-2ЃЉ2+1ЃЌ
ЃЈx-2ЃЉ2+1ЃЌ ЃЈx-2ЃЉ2+1ЃЌЕУЃКy=2ЃЌ
ЃЈx-2ЃЉ2+1ЃЌЕУЃКy=2ЃЌ m2+mЃЉЃЌЕуBЃЈ0ЃЌmЃЉЃЌ
m2+mЃЉЃЌЕуBЃЈ0ЃЌmЃЉЃЌ m2+mЃЉ=
m2+mЃЉ= m2ЃЌ
m2ЃЌ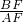 =
=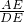 ЃЌМДЃК
ЃЌМДЃК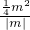 =
=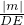 ЃЌ
ЃЌ m2+mЃЉЃЌ
m2+mЃЉЃЌ m2+m+4ЃЉЃЌ
m2+m+4ЃЉЃЌ m2+m+4ЃЌ
m2+m+4ЃЌ •
•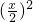 +
+ +4ЃЌ
+4ЃЌ x2+
x2+ x+4ЃЌ
x+4ЃЌ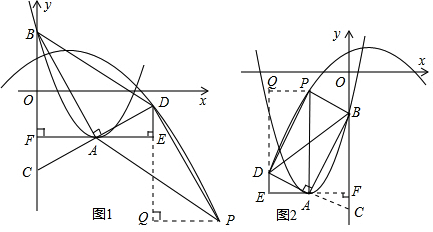
 m2+m+4ЃЉ-ЃЈ
m2+m+4ЃЉ-ЃЈ m2ЃЉ=-
m2ЃЉ=- m2+m+4ЃЌ
m2+m+4ЃЌ m2+m+4ЃЉЕФзјБъДњШыy=-
m2+m+4ЃЉЕФзјБъДњШыy=- x2+
x2+ x+4ЕУЃК
x+4ЕУЃК m2+m+4=-
m2+m+4=- ЁСЃЈ3mЃЉ2+
ЁСЃЈ3mЃЉ2+ ЁСЃЈ3mЃЉ+4ЃЌ
ЁСЃЈ3mЃЉ+4ЃЌ m2+m+4ЃЉ+ЃЈ
m2+m+4ЃЉ+ЃЈ m2ЃЉ=m+4ЃЌ
m2ЃЉ=m+4ЃЌ x2+
x2+ x+4ЕУЃК
x+4ЕУЃК m2+
m2+ m+4ЃЌ
m+4ЃЌ m2+m+4ЃЌНЋm=
m2+m+4ЃЌНЋm= ДњШыy=-
ДњШыy=- m2+m+4ЃЌМДПЩЧѓГіЖўДЮКЏЪ§ЕФБэДяЪНЃЛ
m2+m+4ЃЌМДПЩЧѓГіЖўДЮКЏЪ§ЕФБэДяЪНЃЛ

 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
 ШчЭМЃЌдкЦНУцжБНЧзјБъжаЃЌЫФБпаЮOABCЪЧЕШбќЬнаЮЃЌCBЁЮOAЃЌOA=7ЃЌAB=4ЃЌЁЯCOA=60ЁуЃЌЕуPЮЊxжсЩЯЕФвЛИіЖЏЕуЃЌЕЋЪЧЕуPВЛгыЕу0ЁЂЕуAжиКЯЃЎСЌНгCPЃЌDЕуЪЧЯпЖЮABЩЯвЛЕуЃЌСЌНгPDЃЎ
ШчЭМЃЌдкЦНУцжБНЧзјБъжаЃЌЫФБпаЮOABCЪЧЕШбќЬнаЮЃЌCBЁЮOAЃЌOA=7ЃЌAB=4ЃЌЁЯCOA=60ЁуЃЌЕуPЮЊxжсЩЯЕФвЛИіЖЏЕуЃЌЕЋЪЧЕуPВЛгыЕу0ЁЂЕуAжиКЯЃЎСЌНгCPЃЌDЕуЪЧЯпЖЮABЩЯвЛЕуЃЌСЌНгPDЃЎ| BD |
| AB |
| 5 |
| 8 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
 ЃЈ2012•гхББЧјвЛФЃЃЉШчЭМЃЌдкЦНУцжБНЧзјБъxoyжаЃЌвдзјБъдЕуOЮЊдВаФЃЌ3ЮЊАыОЖЛдВЃЌДгДЫдВФкЃЈАќРЈБпНчЃЉЕФЫљгаећЪ§ЕуЃЈКсЁЂзнзјБъОљЮЊећЪ§ЃЉжаШЮвтбЁШЁвЛИіЕуЃЌЦфКсЁЂзнзјБъжЎКЭЮЊ0ЕФИХТЪЪЧ
ЃЈ2012•гхББЧјвЛФЃЃЉШчЭМЃЌдкЦНУцжБНЧзјБъxoyжаЃЌвдзјБъдЕуOЮЊдВаФЃЌ3ЮЊАыОЖЛдВЃЌДгДЫдВФкЃЈАќРЈБпНчЃЉЕФЫљгаећЪ§ЕуЃЈКсЁЂзнзјБъОљЮЊећЪ§ЃЉжаШЮвтбЁШЁвЛИіЕуЃЌЦфКсЁЂзнзјБъжЎКЭЮЊ0ЕФИХТЪЪЧ| 5 |
| 29 |
| 5 |
| 29 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
 ШчЭМЃЌдкЦНУцжБНЧзјБъжаЃЌЕШбќЬнаЮABCDЕФЯТЕздкxжсЩЯЃЌЧвBЕузјБъЮЊЃЈ4ЃЌ0ЃЉЃЌDЕузјБъЮЊЃЈ0ЃЌ3ЃЉЃЌдђACГЄЮЊ
ШчЭМЃЌдкЦНУцжБНЧзјБъжаЃЌЕШбќЬнаЮABCDЕФЯТЕздкxжсЩЯЃЌЧвBЕузјБъЮЊЃЈ4ЃЌ0ЃЉЃЌDЕузјБъЮЊЃЈ0ЃЌ3ЃЉЃЌдђACГЄЮЊВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
 ШчЭМЃЌдкЦНУцжБНЧзјБъxOyжаЃЌвбжЊЕуAЃЈ-5ЃЌ0ЃЉЃЌPЪЧЗДБШР§КЏЪ§y=
ШчЭМЃЌдкЦНУцжБНЧзјБъxOyжаЃЌвбжЊЕуAЃЈ-5ЃЌ0ЃЉЃЌPЪЧЗДБШР§КЏЪ§y=| k |
| x |
| k |
| x |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
 ЁЯCOA=45ЁуЃЌЖЏЕуPДгЕуOГіЗЂЃЌдкЬнаЮOABCЕФБпЩЯдЫЖЏЃЌТЗОЖЮЊOЁњAЁњBЁњCЃЌЕНДяЕуCЪБЭЃжЙЃЎзїжБЯпCPЃЎ
ЁЯCOA=45ЁуЃЌЖЏЕуPДгЕуOГіЗЂЃЌдкЬнаЮOABCЕФБпЩЯдЫЖЏЃЌТЗОЖЮЊOЁњAЁњBЁњCЃЌЕНДяЕуCЪБЭЃжЙЃЎзїжБЯпCPЃЎВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com