
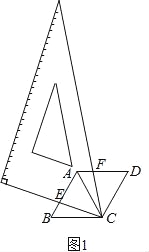
【题目】数学活动课上,某学习小组对有一内角为120°的平行四边形ABCD(∠BAD=120°)进行探究:将一块含60°的直角三角板如图放置在平行四边形ABCD所在平面内旋转,且60°角的顶点始终与点C重合,较短的直角边和斜边所在的两直线分别交线段AB,AD于点E,F(不包括线段的端点).
(1)初步尝试
如图1,若AD=AB,求证:①△BCE≌△ACF,②AE+AF=AC;
(2)类比发现
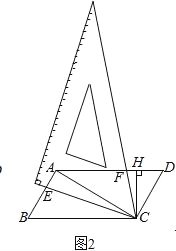
如图2,若AD=2AB,过点C作CH⊥AD于点H,求证:AE=2FH;
(3)深入探究
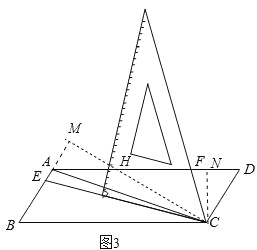
如图3,若AD=3AB,探究得:![]() 的值为常数t,则t= .
的值为常数t,则t= .

【答案】(1)证明过程见解析;(2)证明过程见解析;(3)t=![]()
【解析】
试题分析:(1)①先证明△ABC,△ACD都是等边三角形,再证明∠BCE=∠ACF即可解决问题.②根据①的结论得到BE=AF,由此即可证明.(2)设DH=x,由由题意,CD=2x,CH=![]() x,由△ACE∽△HCF,得
x,由△ACE∽△HCF,得![]() =
=![]() 由此即可证明;(3)如图3中,作CN⊥AD于N,CM⊥BA于M,CM与AD交于点H.先证明△CFN∽△CEM,得
由此即可证明;(3)如图3中,作CN⊥AD于N,CM⊥BA于M,CM与AD交于点H.先证明△CFN∽△CEM,得![]() =
=![]() ,由ABCM=ADCN,AD=3AB,推出CM=3CN,所以
,由ABCM=ADCN,AD=3AB,推出CM=3CN,所以![]() =
=![]() =
=![]() ,设CN=a,FN=b,则CM=3a,EM=3b,想办法求出AC,AE+3AF即可解决问题.
,设CN=a,FN=b,则CM=3a,EM=3b,想办法求出AC,AE+3AF即可解决问题.
试题解析:(1)①∵四边形ABCD是平行四边形,∠BAD=120°, ∴∠D=∠B=60°, ∵AD=AB,
∴△ABC,△ACD都是等边三角形, ∴∠B=∠CAD=60°,∠ACB=60°,BC=AC, ∵∠ECF=60°,
∴∠BCE+∠ACE=∠ACF+∠ACE=60°, ∴∠BCE=∠ACF,
在△BCE和△ACF中,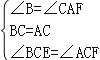 ∴△BCE≌△ACF.
∴△BCE≌△ACF.
②∵△BCE≌△ACF, ∴BE=AF, ∴AE+AF=AE+BE=AB=AC.
(2)设DH=x,由由题意,CD=2x,CH=![]() x, ∴AD=2AB=4x, ∴AH=AD﹣DH=3x, ∵CH⊥AD,
x, ∴AD=2AB=4x, ∴AH=AD﹣DH=3x, ∵CH⊥AD,
∴AC=![]() =2
=2![]() x, ∴AC2+CD2=AD2, ∴∠ACD=90°, ∴∠BAC=∠ACD=90°, ∴∠CAD=30°,
x, ∴AC2+CD2=AD2, ∴∠ACD=90°, ∴∠BAC=∠ACD=90°, ∴∠CAD=30°,
∴∠ACH=60°, ∵∠ECF=60°, ∴∠HCF=∠ACE, ∴△ACE∽△HCF, ∴![]() =
=![]() =2, ∴AE=2FH.
=2, ∴AE=2FH.
(3)如图3中,作CN⊥AD于N,CM⊥BA于M,CM与AD交于点H. ∵∠ECF+∠EAF=180°,
∴∠AEC+∠AFC=180°, ∵∠AFC+∠CFN=180°, ∴∠CFN=∠AEC,∵∠M=∠CNF=90°, ∴△CFN∽△CEM,
∴![]() =
=![]() , ∵ABCM=ADCN,AD=3AB, ∴CM=3CN, ∴
, ∵ABCM=ADCN,AD=3AB, ∴CM=3CN, ∴![]() =
=![]() =
=![]() ,设CN=a,FN=b,则CM=3a,EM=3b,
,设CN=a,FN=b,则CM=3a,EM=3b,
∵∠MAH=60°,∠M=90°, ∴∠AHM=∠CHN=30°, ∴HC=2a,HM=a,HN=![]() a,
a,
∴AM=![]() a,AH=
a,AH=![]() a, ∴AC=
a, ∴AC=![]() =
=![]() a,
a,
AE+3AF=(EM﹣AM)+3(AH+HN﹣FN)=EM﹣AM+3AH+3HN﹣3FN=3AH+3HN﹣AM=![]() a, ∴
a, ∴![]() =
=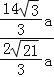 =
=![]() .
.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】将某个图形的各个顶点的横坐标都减去2,纵坐标保持不变,可将该图形( )
A. 向左平移2个单位B. 向右平移2个单位
C. 向上平移2个单位D. 向下平移2个单位
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初二某班12名同学练习定点投篮,每人各投10次,进球数统计如表.这12名同学进球数的众数是( )
进球数(个) | 1 | 2 | 3 | 4 | 5 | 7 |
人数(人) | 1 | 1 | 4 | 2 | 3 | 1 |
A. 3.75B. 3C. 3.5D. 7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2+(2k+1)x+k2+2=0有两个相等的实数根,试判断直线y=(2k﹣3)x﹣4k+12能否通过点A(﹣2,4),并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com