
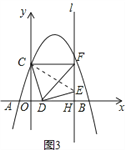
【题目】如图1,在平面直角坐标系中,抛物线y=ax2+bx+4交x轴于A(﹣2,0)和B(8,0)两点,交y轴于点C,点D是线段OB上一动点,连接CD,将线段CD绕点D顺时针旋转90°得到线段DE,过点E作直线l⊥x轴于H,过点C作CF⊥l于F.
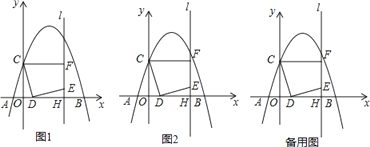
(1)求抛物线解析式;
(2)如图2,当点F恰好在抛物线上时,求线段OD的长;
(3)在(2)的条件下:
①连接DF,求tan∠FDE的值;
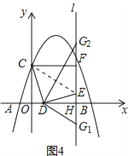
②试探究在直线l上,是否存在点G,使∠EDG=45°?若存在,请直接写出点G的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)OD=2;(3)①tan∠FDE=
;(2)OD=2;(3)①tan∠FDE=![]() ;②存在,点G的坐标为(4,﹣
;②存在,点G的坐标为(4,﹣![]() )或(6,12).
)或(6,12).
【解析】(1)利用待定系数法求得即可;
(2)根据C的纵坐标求得F的坐标,然后通过△OCD≌△HDE,得出DH=OC=3,即可求得OD的长;
(3)①先确定C、D、E、F四点共圆,根据圆周角定理求得∠ECF=∠EDF,可求得tan∠FDE=![]() =
=![]() ;②连接CE,得出△CDE是等腰直角三角形,得出∠CED=45°,过D点作DG1∥CE,交直线l于G1,过D点作DG2⊥CE,交直线l于G2,则∠EDG1=45°,∠EDG2=45°,求得直线CE的解析式为
;②连接CE,得出△CDE是等腰直角三角形,得出∠CED=45°,过D点作DG1∥CE,交直线l于G1,过D点作DG2⊥CE,交直线l于G2,则∠EDG1=45°,∠EDG2=45°,求得直线CE的解析式为![]() ,即可设出直线DG1的解析式为
,即可设出直线DG1的解析式为![]() ,直线DG2的解析式为y=3x+n,把D的坐标代入即可求得m、n,从而求得解析式,进而求得G的坐标.
,直线DG2的解析式为y=3x+n,把D的坐标代入即可求得m、n,从而求得解析式,进而求得G的坐标.
本题解析:(1)如图1,∵抛物线y=ax2+bx+4交x轴于A(﹣2,0)和B(8,0)两点,
∴![]() 解得
解得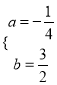 .
.
∴抛物线解析式为: ![]()
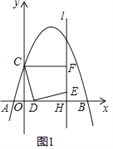
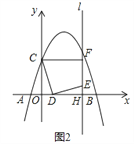
(2)如图2,∵点F恰好在抛物线上,C(0,4), ∴F的纵坐标为4,
把y=4代入![]() , 解得x=0或x=6, ∴F(6,4), ∴OH=6,
, 解得x=0或x=6, ∴F(6,4), ∴OH=6,
∵∠CDE=90°, ∴∠ODC+∠EDH=90°, ∴∠OCD=∠EDH,
在△OCD和△HDE中,
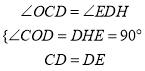 ,
,
∴DH=OC=4, ∴OD=6﹣4=2;
(3)①如图3,连接CE, ∵△OCD≌△HDE, ∴HE=OD=2,
∵BF=OC=4, ∴EF=4﹣2=2,
∵∠CDE=∠CFE=90°,∴C、D、E、F四点共圆, ∴∠ECF=∠EDF,
在RT△CEF中,∵CF=OH=6, ∴tan∠ECF=![]() =
=![]() , ∴tan∠FDE=
, ∴tan∠FDE=![]() ;
;
②如图4,连接CE, ∵CD=DE,∠CDE=90°,∴∠CED=45°,
过D点作DG1∥CE,交直线l于G1,过D点作DG2⊥CE,交直线l于G2,则∠EDG1=45°,∠EDG2=45°
∵EH=2,OH=6, ∴E(6,2),
∵C(0,4), ∴直线CE的解析式为![]() ,
,
设直线DG1的解析式为![]() ,
,
∵D(2,0), ∴![]() ,解得m=
,解得m=![]() , ∴直线DG1的解析式为
, ∴直线DG1的解析式为![]() ,
,
当x=6时, ![]() ∴G1(6,﹣
∴G1(6,﹣![]() );
);
设直线DG2的解析式为y=3x+n,
∵D(2,0), ∴0=3×2+n,解得n=﹣6, ∴直线DG2的解析式为y=3x﹣6,
当x=6时,y=3×6﹣6=12, ∴G2(6,12);
综上,在直线l上,是否存在点G,使∠EDG=45°,点G的坐标为(4,﹣ ![]() )或(6,12).
)或(6,12).


科目:初中数学 来源: 题型:
【题目】一只跳蚤在第一象限及x轴、y轴上跳动,在第一秒钟,它从原点跳动到(0,1),然后接着按图中箭头所示方向跳动,即(0,0)→(0,1)→(1,1)→(1,0)…,且每秒跳动一个单位,那么第35秒时跳蚤所在位置的坐标是( )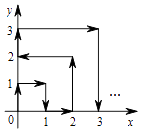
A.(4,0)
B.(5,0)
C.(0,5)
D.(5,5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,每个小正方形的边长都为1,△ABC在网格中的位置如图所示,△ABC的三个顶点都在格点上. 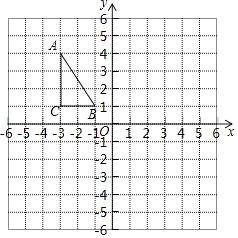
(1)写出△ABC三个顶点的坐标;
(2)将点A,B,C的横坐标都乘以﹣1,纵坐标不变,分别得到点A1 , B1 , C1 , 在图中找到点A1 , B1 , C1 , 并顺次连接A1 , B1 , C1得到△A1B1C1 , 则这两个三角形关于对称;
(3)若以点A,C,P为顶点的三角形与△ABC全等,直接写出所有符合条件的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=2(x-3)2+1.下列说法:
①其图象的开口向下;②其图象的对称轴为直x=3;③其图象顶点坐标为(3,1);④当x<3,y随x的增大而减小.
则其中说法正确的有()
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点A(﹣1,0),B(0,﹣3). 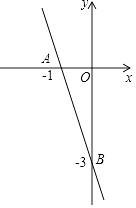
(1)求:直线AB的表达式;
(2)直接写出直线AB向下平移2个单位后得到的直线表达式;
(3)求:在(2)的平移中直线AB在第三象限内扫过的图形面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算。
(1)你发现了吗?( ![]() )2=
)2= ![]() ×
× ![]() ,(
,( ![]() )﹣2=
)﹣2= ![]() =
= ![]() ×
× ![]() =
= ![]() ×
× ![]() 由上述计算,我们发现(
由上述计算,我们发现( ![]() )2(
)2( ![]() )﹣2;
)﹣2;
(2)仿照(1),请你通过计算,判断( ![]() )3与(
)3与( ![]() )﹣3之间的关系.
)﹣3之间的关系.
(3)我们可以发现:( ![]() )﹣m(
)﹣m( ![]() )m(ab≠0)
)m(ab≠0)
(4)计算:( ![]() )﹣4×(
)﹣4×( ![]() )4 .
)4 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某中学初三800名学生的视力情况,从中随机抽取了30名学生进行调查,在此次调查中,样本容量为( )
A.800 B.30 C.800名学生的视力 D.30名学生的视力
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com