
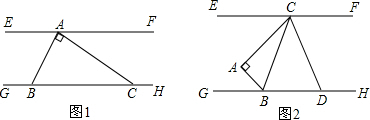
分析 (1)求出∠EAB,推出∠EAB=∠ABC,根据平行线的判定推出即可;
(2)求出AM∥EF∥GH,根据平行线的性质得出∠FCA+∠CAM=180°,∠MAB+∠ABH=180°,∠CBH=∠ECB,求出∠FCA+∠ABH=270°,求出∠FCD+∠ECB=135°,根据三角形内角和定理求出即可.
解答 (1)证明:∵∠EAB=180°-∠BAC-∠FAC,∠BAC=90°,∠FAC=30°,
∴∠EAB=60°,
又∵∠ABC=60°,
∴∠EAB=∠ABC,
∴EF∥GH;
(2)解:不发生变化,
理由是:经过点A作AM∥GH,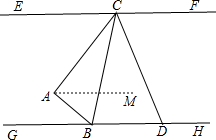
又∵EF∥GH,
∴AM∥EF∥GH,
∴∠FCA+∠CAM=180°,∠MAB+∠ABH=180°,∠CBH=∠ECB,
又∵∠CAM+∠MAB=∠BAC=90°,
∴∠FCA+∠ABH=270°,
又∵BC平分∠ABH,CD平分∠FCA,
∴∠FCD+∠CBH=135°,
又∵∠CBH=∠ECB,即∠FCD+∠ECB=135°,
∴∠BCD=180°-(∠FCD+∠ECB)=45°.
点评 本题考查了三角形内角和定理,平行线的性质和判定的应用,能正确运用定理进行推理是解此题的关键,难度适中.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| A型 | B型 | |
| 价格(万元/台) | 12 | 10 |
| 月污水处理能力(吨/月) | 200 | 160 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
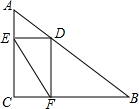 如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,D是AB上一动点,过点D作DE⊥AC于点E,DF⊥BC于点F,连接EF,则线段EF的最小值是( )
如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,D是AB上一动点,过点D作DE⊥AC于点E,DF⊥BC于点F,连接EF,则线段EF的最小值是( )| A. | 2.5 | B. | 2.4 | C. | 2.2 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 这1000名考生是总体的一个样本 | B. | 近2万名考生是总体 | ||
| C. | 每位考生的数学成绩是个体 | D. | 1000名学生是样本容量 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
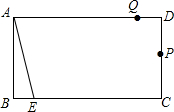 如图,矩形ABCD中,AB=6cm,BC=10cm,动点P从点D出发,按折线DCBAD方向以2cm/s的速度运动,动点Q从点D出发,按折线DABCD方向以1cm/s的速度运动.若点E在线段BC上,且BE=1cm,若动点P、Q同时出发,经过几秒钟,点A、E、P、Q组成平行四边形?
如图,矩形ABCD中,AB=6cm,BC=10cm,动点P从点D出发,按折线DCBAD方向以2cm/s的速度运动,动点Q从点D出发,按折线DABCD方向以1cm/s的速度运动.若点E在线段BC上,且BE=1cm,若动点P、Q同时出发,经过几秒钟,点A、E、P、Q组成平行四边形?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com