
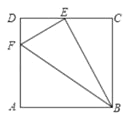
【题目】如图,在边长12的正方形ABCD中,点E是CD的中点,点F在边AD上,且AF=3DF,连接BE,BF,EF,请判断△BEF的形状,并说明理由。
【答案】△BEF是直角三角形,理由见解析
【解析】
因为正方形的四条边相等,边长为12,由E为DC的中点,得出DE和EC的长,AF=3DF,得出AF和DF的长,从而在Rt△ABF中、Rt△BCE中和Rt△DEF中,分别由勾股定理求得BF、BE和EF的长,得到BE2+EF2=BF2,再由勾股定理逆定理证得△BEF是直角三角形.
解:△BEF是直角三角形,理由如下:
∵四边形ABCD是正方形,
∴∠A=∠C=∠D=90°
∵点E是CD的中点,
∴DE=CE=![]() CD=6.
CD=6.
∵AF=3DF,
∴DF=![]() AD=3
AD=3
∴AF=3DF=9.
在Rt△ABF中,由勾股定理可得BF2=AB2+AF2=144+81=225,
在Rt△BCE中,由勾股定理可得BE2=CB2+CE2=144+36=180,
在Rt△DEF中,由勾股定理可得EF2=DF2+DE2=9+36=45,
∵BE2+EF2=180+45=225,BF2=225,
∴BE2+EF2=BF2
∴△BEF是直角三角形.


科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 的边长为4,点
的边长为4,点![]() 是对角线
是对角线![]() 的中点,点
的中点,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 边上运动,且保持
边上运动,且保持![]() ,连接
,连接![]() ,
,![]() ,
,![]() .在此运动过程中,下列结论:①
.在此运动过程中,下列结论:①![]() ;②
;②![]() ;③四边形
;③四边形![]() 的面积保持不变;④当
的面积保持不变;④当![]() 时,
时,![]() ,其中正确的结论是( )
,其中正确的结论是( )
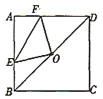
A.①②B.②③C.①②④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() ABCD中, 对角线AC、BD相交于点O. E、F是对角线AC上的两个不同点,当E、F两点满足下列条件时,四边形DEBF不一定是平行四边形( ).
ABCD中, 对角线AC、BD相交于点O. E、F是对角线AC上的两个不同点,当E、F两点满足下列条件时,四边形DEBF不一定是平行四边形( ).

A.AE=CFB.DE=BFC.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
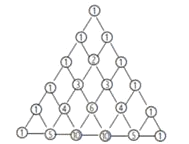
【题目】我国古代数学领域有些研究成果曾位居世界前列,其中“杨辉三角”就是一例.南宋数学家杨辉(约13世纪)所著的《详解九章算术》(1261年)一书中,用图中的三角形解释二项和的乘方规律.杨辉三角两腰上的数都是1,其余每个数都为它的上方(左右)两数之和,这个三角形给出了(a+b)n(n=1,2,3,4,5)的展开式(按a的次数由大到小的顺序)的系数规律.例如,此三角形中第3行的3个数1,2,1,恰好对应着(a+b)2=a2+2ab+b2展开式中各项的系数:第4行的4个数1,3,3,1,恰好对应着(a+b)3=a3+3a2b+3ab2+b2展开式中各项的系数,等等.利用上面呈现的规律填空:(a+b)6=a6+6a5b+________+20a3b3+15a2b4+ ________+b6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线CB∥OA,∠C=∠OAB=120°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF.

(1)求∠EOB的度数.
(2)若平行移动AB,那么∠OBC:∠OFC的值是否随之发生变化? 若变化,找出变化规律或求出变化范围;若不变,求出这个比值.
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA? 若存在,求出∠OBA的度数;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,七(1)班的小明等同学随家长一同到某公园游玩,下面是购买门票时,小明与他爸爸的对话,试根据对话中的信息,解答下列问题:
儿子:爸爸,成人门票是每张20元;学生门票是五折优惠;
团体票(16人及16人以上),按成人票的六折优惠.
爸爸:我们成人、学生一共12人,共需200元.
(1)设小明他们一共去了学生![]() 人,则成人购买门票的总费用为: 元;(用含
人,则成人购买门票的总费用为: 元;(用含![]() 的代数式表示)
的代数式表示)
(2)七(1)班小明他们一共去了几个成人、几个学生?
(3)正在购票时,小明发现七(2)班的小军等10名同学和他们的7名家长共17人也来购票,他们准备联合一起购买门票,请你为这29人的团队设计出最省的购票方案(直接写出方案即可,无需讨论),并求出此时的购票费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
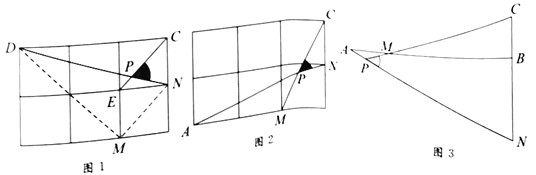
【题目】问题呈现
如图1,在边长为1的正方形网格中,连接格点![]() 、
、![]() 和
和![]() 、
、![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,求
,求![]() 的值.
的值.
方法归纳
求一个锐角的三角函数值,我们往往需要找出(或构造出)一个直角三角形.观察发现问题中![]() 不在直角三角形中,我们常常利用网格画平行线等方法解决此类问题.比如连接格点
不在直角三角形中,我们常常利用网格画平行线等方法解决此类问题.比如连接格点![]() 、
、![]() ,可得
,可得![]() ,则
,则![]() ,连接
,连接![]() ,那么
,那么![]() 就变换到中
就变换到中![]() .
.
问题解决
(1)直接写出图1中![]() 的值为_________;
的值为_________;
(2)如图2,在边长为1的正方形网格中,![]() 与
与![]() 相交于点
相交于点![]() ,求
,求![]() 的值;
的值;
思维拓展
(3)如图3,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() ,延长
,延长![]() 到
到![]() ,使
,使![]() ,连接
,连接![]() 交
交![]() 的延长线于点
的延长线于点![]() ,用上述方法构造网格求
,用上述方法构造网格求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】海洋服装厂生产一种西装和领带,西装每套定价300元,领带每条定价40元![]() 厂方在开展促销活动期间,向客户提供两种优惠方案:
厂方在开展促销活动期间,向客户提供两种优惠方案:![]() 买一套西装送一条领带;
买一套西装送一条领带;![]() 西装和领带定价打9折付款.现有某客户要到该服装厂购买西装50套,领带x条
西装和领带定价打9折付款.现有某客户要到该服装厂购买西装50套,领带x条![]() .
.
(1)若该客户分别按两种优惠方案购买,需付款各多少元![]() 用含x的式子表示
用含x的式子表示![]() .
.
(2)若该客户购买西装50套,领带60条,请通过计算说明按哪种方案购买较为合算.
(3)请通过计算说明什么情况下客户分别选择方案![]() 购买较为合算.
购买较为合算.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com