
����Ŀ�������װ������һ����װ���������װÿ����300Ԫ�����ÿ������40Ԫ![]() �����ڿ�չ������ڼ䣬��ͻ��ṩ�����Żݷ�����
�����ڿ�չ������ڼ䣬��ͻ��ṩ�����Żݷ�����![]() ��һ����װ��һ�������
��һ����װ��һ�������![]() ��װ��������۴�9�۸������ij�ͻ�Ҫ���÷�װ��������װ50�ף����x��
��װ��������۴�9�۸������ij�ͻ�Ҫ���÷�װ��������װ50�ף����x��![]() ��
��
��1�����ÿͻ��ֱ������Żݷ��������踶�������Ԫ![]() �ú�x��ʽ�ӱ�ʾ
�ú�x��ʽ�ӱ�ʾ![]() ��
��
��2�����ÿͻ�������װ50�ף����60������ͨ������˵�������ַ��������Ϊ���㣮
��3����ͨ������˵��ʲô����¿ͻ��ֱ�ѡ��![]() �����Ϊ���㣮
�����Ϊ���㣮
���𰸡���1�������٣�![]() �������ڣ�
�������ڣ�![]() ����2���������ٹ���Ϻ��㣻��3��������
����2���������ٹ���Ϻ��㣻��3��������![]() ʱ��ѡ���ٸ����ʣ����������
ʱ��ѡ���ٸ����ʣ����������![]() ʱ��ѡ���ٺͷ�����һ�������������
ʱ��ѡ���ٺͷ�����һ�������������![]() ʱ��ѡ���ڸ����ʣ�
ʱ��ѡ���ڸ����ʣ�
��������
��1������������Էֱ��ú�x�Ĵ���ʽ��ʾ�����ָ���Ľ�
��2����x=60�ֱ���루1���еĴ���ʽ��Ȼ��Ƚϴ�С�����ɽ���⣻
��3�����ݣ�1���еĴ���ʽ�õ�����40x+13000=36x+13500��ͨ���ⷽ�̵õ�x��ֵ��Ȼ������жϼ��ɣ�
�⣺��1��������ɵã�
�����ٸ���Ϊ��300��50+��x-50����40=��40x+13000����Ԫ����
�����ڸ���Ϊ����300��50+40x����0.9=��13500+36x����Ԫ����
�������ٸ���Ϊ����40x+13000��Ԫ�������ڸ���Ϊ����13500+36x��Ԫ��
��2����x=60ʱ��
�����ٸ���Ϊ��40x+13000=40��60+13000=15400��Ԫ����
�����ڸ���Ϊ��13500+36x=13500+36��60=15660��Ԫ����
��15400��15660��
����ٹ����Ϊ���㣻
��3���裺![]() ��
��
��ã�![]() ��
��
���������![]() ʱ��
ʱ��
![]() ��
��
ѡ���ٸ����ʣ�
���������![]() ʱ��
ʱ��
![]() ��
��
ѡ���ٺͷ�����һ����
���������![]() ʱ��
ʱ��
![]() ��
��
ѡ���ڸ�����.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڱ߳�12��������ABCD�У���E��CD���е㣬��F�ڱ�AD�ϣ���AF=3DF������BE��BF��EF�����ж���BEF����״����˵�����ɡ�
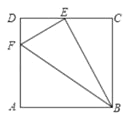
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧΪ�ƶ���ʱ�������� ��Զ��������У�����������ƻ���չ������A����ʷ�ݽ�������B����ʷ�ֳ���������C����ʷ֪ʶ������D����ɫ��ӽ������У��ί��ѧ����ϲ����һ�����е��飬�����ȡ�˲���ѧ�����������������Ƴ�ͼ1��ͼ2������������ͳ��ͼ������ͼ����Ϣ����������⣺
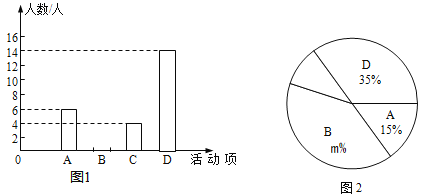
��1�����ι������� ��ѧ������ͼ1������ͳ��ͼ����������
��2������ͳ��ͼ��m=��������ʾ��C��������ε�Բ�Ľ����������ȣ�
��3����֪�ڱ��������ϲ������ʷ֪ʶ��������Ŀ��4��ѧ����ֻ��1��Ů�����ִ���4��ѧ���������ȡ2��ѧ���μӸ���Ŀ���������û���״ͼ���б��ķ��������ǡ�ó鵽һ������һ��Ů���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB��AC����A��36����D��E����ֱ��ڱ�AC��BC�ϣ�BDƽ�֡�ABC��DE��AB��ͼ�еĵ��������ι��У�������
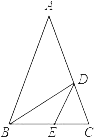
A. 3��B. 4��C. 5��D. 6��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ֱ��MN��ֱ��AB��CD�ֱ��ڵ�E��F����1���2������
��1�����ж�ֱ��AB��ֱ��CD��λ�ù�ϵ����˵�����ɣ�
��2����ͼ2����BEF���EFD�Ľ�ƽ���߽��ڵ�P��EP��CD���ڵ�G����H��MN��һ�㣬��GH��EG����֤��PF��GH��
��3����ͼ3���ڣ�2���������£�����PH��K��GH��һ��ʹ��PHK����HPK����PQƽ�֡�EPK���ʡ�HPQ�Ĵ�С�Ƿ����仯�������䣬�������ֵ�����仯��˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ͼ���ṩ��ůƿ��ˮ�����ۼ���Ϣ���ش��������⣺
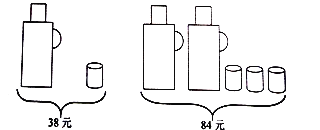
��1��һ��ůƿ��һ��ˮ�����ۼ۷ֱ��Ƕ���Ԫ��
��2���ס��������̳�ͬʱ����ͬ����ůƿ��ˮ�����������ڼ䣬�����̳����ڸ����������̳��涨����������Ʒ����8.5�ۣ����̳��涨��������Ʒ�������ۣ�����һ��ůƿ����һ��ˮ������ij��λ��Ҫ��4��ůƿ��16��ˮ�������������λѡ���ļ��̳���������㣬��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���±���ijУ�ߩ����꼶ij�¿�����ȤС��ʱ��ͳ�Ʊ������и��꼶ͬһ��ȤС��ÿ�λʱ����ͬ���������о��꼶���������ݱ��ڸ��ˣ��ǵþ��꼶����С��������Ƽ�С��������ͬ��
�꼶 | ����С����ʱ�䣨��λ��h�� | ����С������ | �Ƽ�С������ |
���꼶 | 17 | 6 | 8 |
���꼶 | 14.5 | 5 | 7 |
���꼶 | 12.5 |
|
|
����꼶�Ƽ�С���Ĵ�����_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����⣺
��ͼ1�����ı���ABCD�ı�AB����ȡһ��E����E�����A����B�غϣ����ֱ�����ED��EC�������ı���ABCD�ֳ����������Σ�����������������������ƣ����ǾͰ�E�����ı���ABCD�ı�AB�ϵ����Ƶ㣻��������������ζ����ƣ����ǾͰ�E�����ı���ABCD�ı�AB�ϵ�ǿ���Ƶ㣮������⣺
��1����ͼ1����A=��B=��DEC=55�������жϵ�E�Ƿ����ı���ABCD�ı�AB�ϵ����Ƶ㣬��˵�����ɣ�
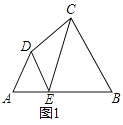
��2����ͼ2���ھ���ABCD�У�AB=5��BC=2����A��B��C��D�ĵ��������������������ÿ��С�����εı߳�Ϊ1���ĸ�㣨��ÿ��С�����εĶ��㣩�ϣ�����ͼ2�л�������ABCD�ı�AB�ϵ�һ��ǿ���Ƶ�E��
��չ̽����

��3����ͼ3��������ABCD��CM�۵���ʹ��D����AB���ϵĵ�E��������Eǡ�����ı���ABCM�ı�AB�ϵ�һ��ǿ���Ƶ㣬��̽��AB��BC��������ϵ��
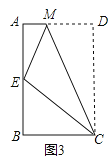
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������龳��
��ͼ1���ı���ABCD�������Σ�M��BC���ϵ�һ�㣬E��CD�ߵ��е㣬AEƽ�֡�DAM����֤��AM=AD+MC��

��̽��չʾ��
��2�����ı���ABCD�dz��������ȵľ��Σ������������䣬��ͼ2�����ж�AM=AD+MC�Ƿ�������������������֤����������������˵�����ɣ�
����չ���죩
��3������2�����ABCD����AB=6��BC=9����AM�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com